
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
分析 把函數看作是動點M(x,ln2x)與動點N(a,2a)之間距離的平方,利用導數求出曲線y=ln2x上與直線y=2x平行的切線的切點,得到曲線上點到直線距離的最小值,結合題意可得只有切點到直線距離的平方等于$\frac{1}{5}$,然后由兩直線斜率的關系列式求得實數a的值.
解答 解:函數f(x)可以看作是動點M(x,ln2x)與動點N(a,2a)之間距離的平方,
動點M在函數y=ln2x的圖象上,N在直線y=2x的圖象上,
問題轉化為求直線上的動點到曲線的最小距離,
由y=ln2x得,y'=$\frac{1}{x}$=2,解得x=$\frac{1}{2}$,
∴曲線上點M($\frac{1}{2}$,0)到直線y=2x的距離最小,
最小距離d=$\frac{1}{\sqrt{5}}$,
則f(x)≥$\frac{1}{5}$,
根據題意,要使f(x0)≤$\frac{1}{5}$,
則f(x0)=$\frac{1}{5}$,此時N恰好為垂足,
由kMN=$\frac{2a-0}{a-\frac{1}{2}}$=$\frac{4a}{2a-1}$=-$\frac{1}{2}$,
解得a=$\frac{1}{10}$.
故選:A.
點評 本題考查利用導數求曲線上過某點切線的斜率,考查了數形結合和數學轉化思想方法,訓練了點到直線的距離公式的應用,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (x-2)2+(y+3)2=36 | B. | (x-2)2+(y+3)2=25 | C. | (x-2)2+(y+3)2=18 | D. | (x-2)2+(y+3)2=9 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
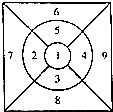 如圖,圖案共分9個區域,有6種不同顏色的涂料可供涂色,每個區域只能涂一種顏色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相鄰區域的顏色不相同,則涂色方法有( )
如圖,圖案共分9個區域,有6種不同顏色的涂料可供涂色,每個區域只能涂一種顏色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相鄰區域的顏色不相同,則涂色方法有( )| A. | 360種 | B. | 720種 | C. | 780種 | D. | 840種 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知平面α∩β=l,點A∈α,點B∈α,點C∈β,且A∉l,B∉l,直線AB與l不平行,那么平面ABC與平面β的交線與l有什么關系?證明你的結論.
如圖,已知平面α∩β=l,點A∈α,點B∈α,點C∈β,且A∉l,B∉l,直線AB與l不平行,那么平面ABC與平面β的交線與l有什么關系?證明你的結論.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com