
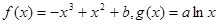 .
.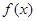 在
在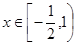 上的最大值為
上的最大值為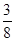 ,求實數
,求實數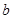 的值;
的值;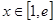 ,都有
,都有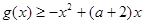 恒成立,求實數
恒成立,求實數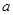 的取值范圍;
的取值范圍;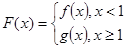 ,對任意給定的正實數
,對任意給定的正實數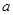 ,曲線
,曲線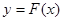 上是否存在兩點
上是否存在兩點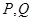 ,使得
,使得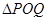 是以
是以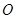 (
(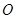 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在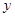 軸上?請說明理由.
軸上?請說明理由.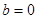 .(Ⅱ)
.(Ⅱ) .
.  ,曲線
,曲線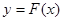 上總存在兩點
上總存在兩點 ,
, ,使得
,使得 是以
是以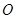 (
(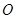 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上.
軸上.  ,得
,得 ,
, ,得
,得 或
或 .
. 變化時,
變化時, 及
及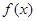 的變化如下表:
的變化如下表: |  |  |  |  |  |  |
 | | - |  | + |  | - |
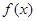 |  | ↘ | 極小值 | ↗ | 極大值 | ↘ |
 ,
,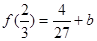 ,
, ,
, ,
, . 4分
. 4分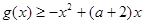 ,得
,得 .
. ,且等號不能同時取,
,且等號不能同時取, ,即
,即
 恒成立,即
恒成立,即 . 6分
. 6分 ,求導得,
,求導得, ,
, 時,
時, ,從而
,從而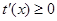 ,
, 在
在 上為增函數,
上為增函數, ,
, . 8分
. 8分
 ,
,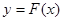 上存在兩點
上存在兩點 ,
, 滿足題意,則
滿足題意,則 ,
, 只能在
只能在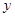 軸兩側,
軸兩側, ,則
,則 ,且
,且 .
. 是以
是以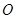 為直角頂點的直角三角形,
為直角頂點的直角三角形, ,
,
 ,
, ,
, 等價于方程
等價于方程 在
在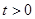 且
且 時是否有解. 10分
時是否有解. 10分 時,方程
時,方程 為
為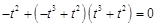 ,化簡得
,化簡得 ,此方程無解;
,此方程無解; 時,方程
時,方程 為
為 ,即
,即 ,
, ,則
,則 ,
, 時,
時, ,
, 在
在 上為增函數,
上為增函數, 的值域為
的值域為 ,即
,即 ,
, 當
當 時,方程
時,方程 總有解.
總有解. 對任意給定的正實數
對任意給定的正實數 ,曲線
,曲線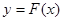 上總存在兩點
上總存在兩點 ,
, ,使得
,使得 是以
是以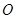 (
( 為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上. 14分
軸上. 14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com