【題目】如圖，已知四棱錐
中，平面
平面
，平面
平面，
為
上任意一點，
為菱形對角線的交點。
（1）證明：平面
平面
；
（2）若
，當(dāng)四棱錐的體積被平面
分成3：1兩部分時，若二面角
的大小為
，求
的值。
【答案】（1）見解析（2）
【解析】
（1）通過在面內(nèi)作交線的垂線，和面面垂直性質(zhì)定理證明
面ABCD，再通過
面PDB,證明平面
平面
。（2）設(shè)三棱錐
的高為
，由體積比可得
，故此時
為
的中點。可證面面
。過點
作
于點
，連接
，則
，故
即為二面角
的平面角，即
。進一步求的
的值。方法二是利用空量向量求得比值。
（1）過點
作
于點G，由于平面
面，所以
面
面，故
；同理，過點作
于
，則
面，
面,且
所以面ABCD。所以
，又
，
故面，所以面面面。
（2）若四棱錐的體積被面
分成3：1兩部分，則的體積是整個四棱錐體積的
，設(shè)三棱錐的高為，則
（
為菱形的面積），所以，故此時為的中點，此時
，并且
，故面面，故
面，
，
過點作于點，則
面
，連接，則，故
即為二面角的平面角，即
設(shè)
，則
，
在
中，
，故
，
可解得
，故
解法二：如圖建立坐標(biāo)系，設(shè)
則
，設(shè)
則
面
的法向量為
，設(shè)面面
的法向量為
，則
，取
，則
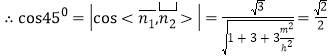
巧學(xué)巧練系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】全國糖酒商品交易會將在四川舉辦.展館附近一家川菜特色餐廳為了研究參會人數(shù)與本店所需原材料數(shù)量的關(guān)系，在交易會前查閱了最近5次交易會的參會人數(shù)
（萬人）與餐廳所用原材料數(shù)量
（袋），得到如下數(shù)據(jù)：
舉辦次數(shù) | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
參會人數(shù) | 11 | 9 | 8 | 10 | 12 |
原材料 | 28 | 23 | 20 | 25 | 29 |
（Ⅰ）請根據(jù)所給五組數(shù)據(jù)，求出關(guān)于的線性回歸方程
；
（Ⅱ）若該店現(xiàn)有原材料12袋，據(jù)悉本次交易會大約有13萬人參加，為了保證原材料能夠滿足需要，則該店應(yīng)至少再補充原材料多少袋？
（參考公式：
，
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在一個文藝比賽中，12名專業(yè)人士和12名觀眾代表各組成一個評委小組，給參賽選手打分，下面是兩組評委對同一名選手的打分：
小組A 42 45 48 46 52 47 49 55 42 51 47 45
小組B 55 36 70 66 75 49 46 68 42 62 58 47
（1）選擇一個可以度量每一組評委打分相似性的量，并對每組評委的打分計算度量值.
（2）你能據(jù)此判斷小組A和小組B中哪一個更像是由專業(yè)人土組成的嗎？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
，橢圓的短軸端點與雙曲線
的焦點重合，過點
的直線
與橢圓
相交于
、
兩點.
(1)求橢圓的方程；
(2)若以
為直徑的圓過坐標(biāo)原點
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)拋物線
的準(zhǔn)線與
軸交于
，拋物線的焦點
，以
為焦點，離心率
的橢圓與拋物線的一個交點為
；自
引直線交拋物線于
兩個不同的點，設(shè)
.
（1）求拋物線的方程橢圓的方程；
（2）若
，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
與
（
為常數(shù)）的圖象在它們與坐標(biāo)軸交點處的切線互相平行.
（1）若關(guān)于
的不等式
有解，求實數(shù)
的取值范圍；
（2）對于函數(shù)
和
公共定義域內(nèi)的任意實數(shù)
，我們把
的值稱為兩函數(shù)在處的“瞬間距離”.則函數(shù)
與
的所有“瞬間距離”是否都大于2？請加以證明.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
