
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,且
,且![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)詳見解析;(2)![]()
【解析】
(1)對函數![]() 求導,分
求導,分![]() ,
,![]() 和
和![]() 三種情況,討論導函數的正負,進而可得到函數
三種情況,討論導函數的正負,進而可得到函數![]() 的單調性;
的單調性;
(2)由(1)知![]() 時,
時,![]() 有兩個極值點,可得
有兩個極值點,可得![]() ,
,![]() ,整理可得
,整理可得![]() ,不等式可化為
,不等式可化為![]() ,結合
,結合![]() 可得到
可得到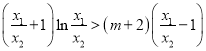 ,令
,令![]() 上述不等式等價于當
上述不等式等價于當![]() 時
時![]() 恒成立,構造函數
恒成立,構造函數![]() ,求導并討論單調性,使其最小值大于0即可求出答案.
,求導并討論單調性,使其最小值大于0即可求出答案.
(1)函數![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
①若![]() ,則
,則![]() ,顯然
,顯然![]() ,所以
,所以![]() 在
在![]() 單調遞減;
單調遞減;
②若![]() ,由
,由![]() 得
得![]() ,此時
,此時![]() ,
,
由![]() 得
得![]() ;
;
由![]() 得
得![]() .
.
即![]() 在區間
在區間![]() 單調遞增,在區間
單調遞增,在區間![]() 和
和![]() 單調遞減;
單調遞減;
③若![]() ,
,![]() ,
,
則![]() 在區間
在區間![]() 單調遞增,在區間
單調遞增,在區間![]() 單調遞減.
單調遞減.
(2)由(1)知![]() 時,
時,![]() 有兩個極值點,
有兩個極值點,![]() ,
,![]() 是方程
是方程![]() 的兩個根,
的兩個根,![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
所以原不等式等價于![]() ,
,
又![]() ,∴
,∴![]() ,
,
即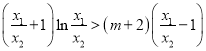 ,
,
令![]() ,上述不等式可化為,當
,上述不等式可化為,當![]() 時,
時,![]() 恒成立.
恒成立.
設![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 時,
時,![]() .
.
①當![]() 即
即![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 符合題意;
符合題意;
②當![]() 時,因為
時,因為![]() 在
在![]() 上單調遞增,記
上單調遞增,記![]() ,
,
則![]() 時
時![]() ,
,![]() 時
時![]() ,
,
即![]() 時
時![]() 單調遞減,所以存在
單調遞減,所以存在![]() ,使
,使![]() ,不合題意,
,不合題意,
綜上所述:![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 為等邊三角形,
為等邊三角形,![]() 為等腰直角三角形,
為等腰直角三角形,![]() .平面
.平面![]() 平面ABD,點E與點D在平面ABC的同側,且
平面ABD,點E與點D在平面ABC的同側,且![]() ,
,![]() .點F為AD中點,連接EF.
.點F為AD中點,連接EF.
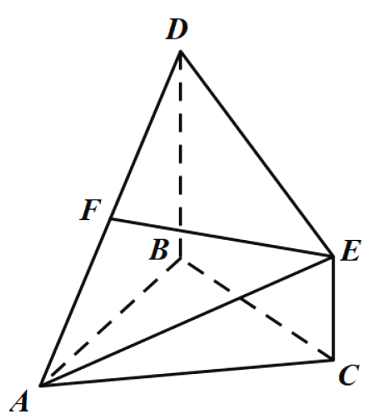
(1)求證:![]() 平面ABC;
平面ABC;
(2)求證:平面![]() 平面ABD.
平面ABD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由我國引領的5G時代已經到來,5G的發展將直接帶動包括運營、制造、服務在內的通信行業整體的快速發展,進而對![]() 增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
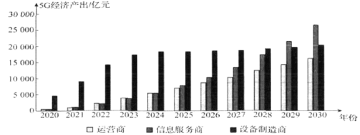
A.5G的發展帶動今后幾年的總經濟產出逐年增加
B.設備制造商的經濟產出前期增長較快,后期放緩
C.設備制造商在各年的總經濟產出中一直處于領先地位
D.信息服務商與運營商的經濟產出的差距有逐步拉大的趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
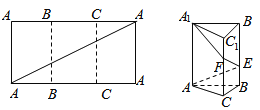
【題目】如圖,把長為6,寬為3的矩形折成正三棱柱![]() ,三棱柱的高度為3,矩形的對角線和三棱柱的側棱
,三棱柱的高度為3,矩形的對角線和三棱柱的側棱![]() 的交點記為E,F.
的交點記為E,F.
(1)求三棱柱![]() 的體積;
的體積;
(2)求三棱柱中異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知有窮數列![]() 共有
共有![]() 項
項![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,試寫出一個滿足條件的數列
,試寫出一個滿足條件的數列![]() ;
;
(2)若![]() ,
,![]() ,求證:數列
,求證:數列![]() 為遞增數列的充要條件是
為遞增數列的充要條件是![]() ;
;
(3)若![]() ,則
,則![]() 所有可能的取值共有多少個?請說明理由.
所有可能的取值共有多少個?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com