
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源:2013-2014學年福建省高考考前模擬文科數學試卷(解析版) 題型:解答題
如圖,設橢圓 的左右焦點為
的左右焦點為 ,上頂點為
,上頂點為 ,點
,點 關于
關于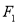 對稱,且
對稱,且
(1)求橢圓 的離心率;
的離心率;
(2)已知 是過
是過 三點的圓上的點,若
三點的圓上的點,若 的面積為
的面積為 ,求點
,求點 到直線
到直線 距離的最大值。
距離的最大值。

查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試理科數學試卷(解析版) 題型:解答題
如圖1,直角梯形 中,
中, ,
, ,
, ,點
,點 為線段
為線段 上異于
上異于 的點,且
的點,且 ,沿
,沿 將面
將面 折起,使平面
折起,使平面 平面
平面 ,如圖2.
,如圖2.
(1)求證: 平面
平面 ;
;
(2)當三棱錐 體積最大時,求平面
體積最大時,求平面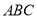 與平面
與平面 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試文科數學試卷(解析版) 題型:選擇題
設向量 與
與 滿足
滿足 ,
, 在
在 方向上的投影為
方向上的投影為 ,若存在實數
,若存在實數 ,使得
,使得 與
與 垂直,則
垂直,則 =( )
=( )
A. B.1 C. 2 D. 3
B.1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查理科數學試卷(解析版) 題型:解答題
已知在平面直角坐標系 中,圓
中,圓 的方程為
的方程為 .以原點
.以原點 為極點,以
為極點,以 軸正半軸為極軸,且與直角坐標系取相同的單位長度,建立極坐標系,直線
軸正半軸為極軸,且與直角坐標系取相同的單位長度,建立極坐標系,直線 的極坐標方程為
的極坐標方程為 .
.
(1)求直線 的直角坐標方程和圓
的直角坐標方程和圓 的參數方程;
的參數方程;
(2)求圓 上的點到直線
上的點到直線 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查理科數學試卷(解析版) 題型:填空題
對于集合 ,如果定義了一種運算“
,如果定義了一種運算“ ”,使得集合
”,使得集合 中的元素間滿足下列4個條件:
中的元素間滿足下列4個條件:
(ⅰ) ,都有
,都有 ;
;
(ⅱ) ,使得對
,使得對 ,都有
,都有 ;
;
(ⅲ) ,
,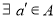 ,使得
,使得 ;
;
(ⅳ) ,都有
,都有 ,
,
則稱集合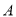 對于運算“
對于運算“ ”構成“對稱集”.
”構成“對稱集”.
下面給出三個集合及相應的運算“ ”:
”:
① ,運算“
,運算“ ”為普通加法;
”為普通加法;
② ,運算“
,運算“ ”為普通減法;
”為普通減法;
③ ,運算“
,運算“ ”為普通乘法.
”為普通乘法.
其中可以構成“對稱集”的有 .(把所有正確的序號都填上)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查文科數學試卷(解析版) 題型:解答題
(已知拋物線 (
(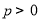 )的準線與
)的準線與 軸交于點
軸交于點 .
.
(1)求拋物線的方程,并寫出焦點坐標;
(2)是否存在過焦點的直線 (直線與拋物線交于點
(直線與拋物線交于點 ,
, ),使得三角形
),使得三角形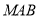 的面積
的面積 ?若存在,請求出直線
?若存在,請求出直線 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年甘肅省武威市高三數學專題訓練選擇填空限時練六(解析版) 題型:選擇題
已知點F1、F2分別是雙曲線 =1(a>0,b>0)的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A,B兩點,若△ABF2是銳角三角形,則該雙曲線離心率的取值范圍是( )
=1(a>0,b>0)的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A,B兩點,若△ABF2是銳角三角形,則該雙曲線離心率的取值范圍是( )
A.(1, ) B.(
) B.( ,2
,2 )
)
C.(1+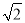 ,+∞) D.(1,1+
,+∞) D.(1,1+ )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com