
【題目】已知函數f(x)=e﹣x﹣ ![]() .
.
(Ⅰ)證明:當x∈[0,3]時, ![]() .
.
(Ⅱ)證明:當x∈[2,3]時, ![]() .
.
【答案】證明:(Ⅰ)要證 ![]() ,也即證ex≤1+9x.
,也即證ex≤1+9x.
令F(x)=ex﹣9x﹣1,則F′(x)=ex﹣9.令F′(x)>0,則x>2ln3.
∴當0≤x<2ln3時,有F′(x)<0,∴F(x)在[0,2ln3]上單調遞減,
2ln3<x≤3時,有F′(x)>0,∴F(x)在[2ln3,3]上單調遞增.
∴F(x)在[0,3]上的最大值為max{F(0),F(3)}.
又F(0)=0,F(3)=e3﹣28<0.
∴F(x)≤0,x∈[0,3]成立,即ex≤1+9x,x∈[0,3]成立.
∴當x∈[0,3]時, ![]() .
.
(Ⅱ)由(I)得:當x∈[2,3]時,f(x)= ![]() ≥
≥ ![]() ,
,
令 ![]() ,
,
則t′(x)=﹣(1+9x)﹣29+(1+x)﹣2
= ![]()
= ![]()
= ![]() ≥0,x∈[2,3].
≥0,x∈[2,3].
∴t(x)在[2,3]上單調遞增,即t(x)≥t(2)=﹣ ![]() =﹣
=﹣ ![]() ,x∈[2,3].
,x∈[2,3].
∴f(x)>﹣ ![]() 得證.
得證.
下證f(x)<0.即證ex>x+1,
令h(x)=ex﹣(x+1),則h′(x)=ex﹣1>0,∴h(x)在[2,3]上單調遞增,
∴h(x)=ex﹣(x+1)≥e2﹣3>0,得證.
∴當x∈[2,3]時, ![]()
【解析】(Ⅰ)要證 ![]() ,即證ex≤1+9x,令F(x)=ex﹣9x﹣1,則F′(x)=ex﹣9,推導出F(x)在[0,3]上的最大值為max{F(0),F(3)}.由此能證明當x∈[0,3]時,
,即證ex≤1+9x,令F(x)=ex﹣9x﹣1,則F′(x)=ex﹣9,推導出F(x)在[0,3]上的最大值為max{F(0),F(3)}.由此能證明當x∈[0,3]時, ![]() .
.
(Ⅱ)當x∈[2,3]時,f(x)= ![]() ≥
≥ ![]() ,令
,令 ![]() ,則t′(x)=
,則t′(x)= ![]() ≥0,x∈[2,3],由此能證明f(x)>﹣
≥0,x∈[2,3],由此能證明f(x)>﹣ ![]() ,證明f(x)<0,即證ex>x+1,令h(x)=ex﹣(x+1),則h′(x)=ex﹣1>0,由此能證明h(x)=ex﹣(x+1)≥e2﹣3>0.
,證明f(x)<0,即證ex>x+1,令h(x)=ex﹣(x+1),則h′(x)=ex﹣1>0,由此能證明h(x)=ex﹣(x+1)≥e2﹣3>0.
【考點精析】掌握函數的最大(小)值與導數是解答本題的根本,需要知道求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】已知直線l經過直線2x+y-5=0與x-2y=0的交點P.
(1)點A(5,0)到直線l的距離為3,求直線l的方程;
(2)求點A(5,0)到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中有20個大小相同的球,其中記上0號的有10個,記上n號的有n個(n=1,2,3,4),現從袋中任取一球,X表示所取球的標號.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,試求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=log2x+ax+b(a>0),若存在實數b,使得對任意的x∈[t,t+2](t>0)都有|f(x)|≤1+a,則t的最小值是( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l過定點P(0,1),且與直線l1:x-3y+10=0,l2:2x+y-8=0分別交于A、B兩點.若線段AB的中點為P,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F為雙曲線 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )
=1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( ) 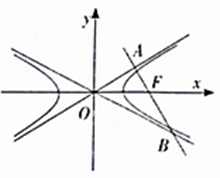
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設某設備的使用年限x(年)和所支出的維修費用y(萬元)有如下的統計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
試求:(1)y與x之間的回歸方程;
(2)當使用年限為10年時,估計維修費用是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ∈[1,+∞).
∈[1,+∞).
(1)當![]() 時,判斷函數
時,判斷函數![]() 的單調性并證明;
的單調性并證明;
(2)當![]() 時,求函數
時,求函數![]() 的最小值;
的最小值;
(3)若對任意![]() ∈[1,+∞),
∈[1,+∞),![]() >0恒成立,試求實數
>0恒成立,試求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com