
【題目】已知等腰梯形ABCD(如圖1所示),其中AB∥CD,E,F分別為AB和CD的中點,且AB=EF=2,CD=6,M為BC中點.現將梯形ABCD沿著EF所在直線折起,使平面EFCB⊥平面EFDA(如圖2所示),N是線段CD上一動點,且![]() .
.

(1)求證:MN∥平面EFDA;
(2)求三棱錐A-MNF的體積.
【答案】(1)見解析;(2)1
【解析】(1)證明:過點M作MP⊥EF于點P,過點N作NQ⊥FD于點Q,連接PQ.由題知,平面EFCB⊥平面EFDA,
又MP⊥EF,平面EFCB∩平面EFDA=EF,
∴MP⊥平面EFDA.
又EF⊥CF,EF⊥DF,CF∩DF=F,
∴EF⊥平面CFD.
又NQ平面CFD,∴NQ⊥EF.
又NQ⊥FD,EF∩FD=F,
∴NQ⊥平面EFDA,
∴MP∥NQ.
又CN=![]() ND,∴NQ=
ND,∴NQ=![]() CF=
CF=![]() ×3=2,
×3=2,
且MP=![]() (BE+CF)=
(BE+CF)=![]() ×(1+3)=2,
×(1+3)=2,
∴MP綊NQ,∴四邊形MNQP為平行四邊形.
∴MN∥PQ.
又∵MN平面EFDA,PQ平面EFDA,
∴MN∥平面EFDA.
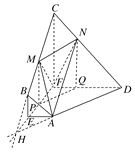
(2)延長DA,CB相交于一點H,則H∈CB,H∈DA.
又∵CB平面FEBC,DA平面FEAD.
∴H∈平面FEBC,H∈平面FEAD,
即H∈平面FEBC∩平面FEAD=EF,
∴DA,FE,CB交于一點H,且HE=![]() EF=1.
EF=1.
V三棱錐F-CDH=V三棱錐C-HFD=![]() ·S△HFD·CF=
·S△HFD·CF=![]() ,
,
又由平面幾何知識得![]() ,則
,則![]() ,
,
∴V三棱錐A-MNF=V三棱錐F-AMN=![]() V三棱錐F-CDH=
V三棱錐F-CDH=![]() =1.
=1.


科目:高中數學 來源: 題型:
【題目】橢圓![]() (
(![]() )的離心率是
)的離心率是![]() ,點
,點![]() 在短軸
在短軸![]() 上,且
上,且![]() 。
。
(1)球橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,過點
為坐標原點,過點![]() 的動直線與橢圓交于
的動直線與橢圓交于![]() 兩點。是否存在常數
兩點。是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若
,若![]() ,則稱
,則稱![]() 為
為![]() 的“不動點”;若
的“不動點”;若![]() ,則稱
,則稱![]() 為
為![]() 的“穩定點”.函數
的“穩定點”.函數![]() 的“不動點”和“穩定點”的集合分別記為
的“不動點”和“穩定點”的集合分別記為![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )設函數
)設函數![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求證:
)求證:![]() .
.
(![]() )設函數
)設函數![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體QPABCD為一簡單組合體,在底面ABCD中,∠DAB=60°,AD⊥DC,AB⊥BC,QD⊥平面ABCD,PA∥QD,PA=1,AD=AB=QD=2.

(1)求證:平面PAB⊥平面QBC;
(2)求該組合體QPABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為(0,+∞),且對一切x>0,y>0都有![]() ,當
,當![]() 時,有
時,有![]()
(1)求f(1)的值;
(2)判斷f(x)的單調性并加以證明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com