
【題目】已知橢圓![]() 的短軸長為2,且橢圓
的短軸長為2,且橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的上焦點作相互垂直的弦
的上焦點作相互垂直的弦![]() ,
,![]() ,求
,求![]() 為定值.
為定值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由題意得到b,a,即可得結果.
(2)通過分直線AB、CD中有一個斜率不存在與均存在兩種情況討論.當直線AB、CD中有一個斜率不存在時,通過計算可知|AB|=![]() 、|CD|=
、|CD|=![]() ,進而可得結論;當直線AB、CD斜率均存在時,設直線AB方程為:y=k(x
,進而可得結論;當直線AB、CD斜率均存在時,設直線AB方程為:y=k(x![]() ),則直線CD方程為:y
),則直線CD方程為:y![]() (x
(x![]() ),通過聯立直線與橢圓方程、利用韋達定理、兩點間距離公式計算可知|AB|
),通過聯立直線與橢圓方程、利用韋達定理、兩點間距離公式計算可知|AB|![]() ,進而計算可得結論.
,進而計算可得結論.
(1)由題意可知![]() ,
,![]() .又橢圓
.又橢圓![]() 的離心率為
的離心率為![]() ,則
,則![]() ,
,
故橢圓![]() 的方程為
的方程為![]()
(2)當直線![]() 的斜率不存在或為零時,
的斜率不存在或為零時,![]()
當直線![]() 的斜率存在,且不為零時,設直線
的斜率存在,且不為零時,設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,
聯立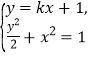 消去
消去![]() ,整理得
,整理得![]() ,
,
則![]() ,
,![]() ,
,
故![]()
![]() .
.
同理可得:![]() ,
,
∴![]()
![]()


科目:高中數學 來源: 題型:
【題目】為保護農民種糧收益,促進糧食生產,確保國家糧食安全,調動廣大農民糧食生產的積極性,從2004年開始,國家實施了對種糧農民直接補貼.通過對2014~2018年的數據進行調查,發現某地區發放糧食補貼額![]() (億元)與該地區糧食產量
(億元)與該地區糧食產量![]() (萬億噸)之間存在著線性相關關系.統計數據如下表:
(萬億噸)之間存在著線性相關關系.統計數據如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
補貼額 | 9 | 10 | 12 | 11 | 8 |
糧食產量 | 23 | 25 | 30 | 26 | 21 |
(1)請根據如表所給的數據,求出![]() 關于
關于![]() 的線性回歸直線方程
的線性回歸直線方程![]() ;
;
(2)通過對該地區糧食產量的分析研究,計劃2019年在該地區發放糧食補貼額7億元,請根據(1)中所得的線性回歸直線方程,預測2019年該地區的糧食產量.
(參考公式: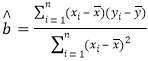 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中![]() 中,直線
中,直線![]() ,圓
,圓![]() 的參數方程為
的參數方程為![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求直線![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等腰梯形ABCD(如圖1所示),其中AB∥CD,E,F分別為AB和CD的中點,且AB=EF=2,CD=6,M為BC中點.現將梯形ABCD沿著EF所在直線折起,使平面EFCB⊥平面EFDA(如圖2所示),N是線段CD上一動點,且![]() .
.

(1)求證:MN∥平面EFDA;
(2)求三棱錐A-MNF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 關于直線
關于直線![]() 對稱的點
對稱的點![]() 位于拋物線
位于拋物線![]() 上.
上.
(1)求拋物線![]() 的方程;
的方程;
(2)設拋物線![]() 的準線與其對稱軸的交點為
的準線與其對稱軸的交點為![]() ,過點
,過點![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于點
于點![]() ,
, ![]() ,直線
,直線![]() 交拋物線
交拋物線![]() 于另一點
于另一點![]() ,求直線
,求直線![]() 所過的定點.
所過的定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線 (
(![]() 為參數),曲線
為參數),曲線 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立直角坐標系.
軸的正半軸為極軸建立直角坐標系.
(1)求曲線![]() 的極坐標方程,直線
的極坐標方程,直線![]() 的普通方程;
的普通方程;
(2)把直線![]() 向左平移一個單位得到直線
向左平移一個單位得到直線![]() ,設
,設![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,
, ![]() ,
, ![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某工廠生產線上隨機抽取16件零件,測量其內徑數據從小到大依次排列如下:1.12,1.25,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.據此可估計該生產線上大約有25%的零件內徑小于等于___________㎜,大約有30%的零件內徑大于___________mm(單位:mm).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 滿足(1)對于定義域上的任意
滿足(1)對于定義域上的任意![]() ,恒有
,恒有![]() ;(2)對于定義域上的任意
;(2)對于定義域上的任意![]() 當
當![]() 時,恒有
時,恒有![]() ,則稱函數
,則稱函數![]() 為“理想函數”,給出下列四個函數中:①
為“理想函數”,給出下列四個函數中:① ![]() ; ②
; ②![]() ;③
;③![]() ;④
;④ ,則被稱為“理想函數”的有( )
,則被稱為“理想函數”的有( )
A.①B.②④C.③D.④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com