
科目:高中數學 來源:湖北省荊州中學2008高考復習立體幾何基礎題題庫一(有詳細答案)人教版 人教版 題型:044
已知:如下圖,P是正方形ABCD所在平面外一點,PA=PB=PC=PD=a,AB=a.
求:平面APB與平面CPD相交所成較大的二面角的余弦值.

查看答案和解析>>
科目:高中數學 來源:重慶市37中2005-2006年高二下第一次月考數學試題 題型:044
如下圖:已知P是正方形ABCD所在平面外一點,點P在平面ABCD內的射影O是正方形的中心,PO=OD=a,E是PD的中點
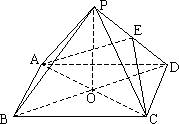
(1)求證:PD⊥平面AEC
(2)求直線BP到平面AEC的距離
(3)求直線BC與平面AEC所成的角
查看答案和解析>>
科目:高中數學 來源: 題型:
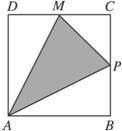
點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A—B—C—M運動時,以點P經過的路程x為自變量,三角形APM的面積為y的函數,則y=f(x)的圖象形狀大致是下列中的( )
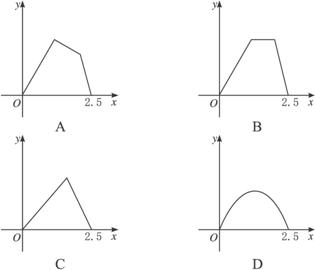
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南省信陽市畢業班第一次調研考試文科數學試卷 題型:解答題
(本小題滿分12分)請你設計一個包裝盒,如下圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A、B、C、D四個點重合于圖中的點P,正好形成一個正四棱挪狀的包裝盒E、F在AB上,是被切去的一等腰直角三角形斜邊的兩個端點.設AE= FB=x(cm).

(I)某廣告商要求包裝盒的側面積S(cm2)最大,試問x應取何值?
(II)某廠商要求包裝盒的容積V(cm3)最大,試問x應取何值?并求出此時包裝盒的高與底面邊長的比值.[
查看答案和解析>>
科目:高中數學 來源: 題型:
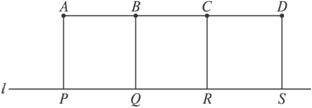
A.P點 B.Q點 C.R點 D.S點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com