
【題目】已知正方體![]() ,過對角線
,過對角線![]() 作平面
作平面![]() 交棱
交棱![]() 于點E,交棱
于點E,交棱![]() 于點F,則:
于點F,則:
①四邊形![]() 一定是平行四邊形;
一定是平行四邊形;
②四邊形![]() 有可能為正方形;
有可能為正方形;
③四邊形![]() 在底面
在底面![]() 內的投影一定是正方形;
內的投影一定是正方形;
④平面![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
其中所有正確結論的序號為( )
A.①②B.②③④C.①④D.①③④
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,點E是SD上的點,且DE=![]() a(0<
a(0<![]() ≦1). w.w.w..c.o.m
≦1). w.w.w..c.o.m
(Ⅰ)求證:對任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小為600C,求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】同學們有沒有讀過莎士比亞的名劇《威尼斯商人》?數學家斯摩林在劇中增加了一個情節:安東尼奧到鮑西婭家向她求婚,鮑西婭拿出一金、一銀、一鋁三個盒子,說:“每只盒子上寫了一句話,但只有一句是真的.誰能猜中我的肖象在哪只盒子中,才能做我的丈夫”.如果你是聰明、政治的安東尼奧,請問肖象在哪個盒子內?(請從金盒、銀盒、鋁盒中選擇一個填在橫線上)________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知多面體ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(Ⅰ)證明:AB1⊥平面A1B1C1;
(Ⅱ)求直線AC1與平面ABB1所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知矩形ABCD所在平面垂直直角梯形ABPE所在的平面于直線AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
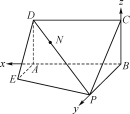
(1)求平面PCD與平面ABPE所成的二面角的余弦值;
(2)在線段PD上是否存在一點N,使得直線BN與平面PCD所成角的正弦值等于![]() ?若存在,試確定點N的位置;若不存在,請說明理由.
?若存在,試確定點N的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com