Question

（09年宣武區二模理）（13分）

如圖，在正三棱柱ABC―A₁B₁C₁中，BB­₁=BC=2，且M是BC的中點，點N在CC₁上。

   （1）試確定點N的位置，使AB₁⊥MN；

   （2）當AB₁⊥MN時，求二面角M―AB₁―N的大小。

Answer 1

解析：解法1：（1）連結MA、B₁M，過M作MN⊥B₁M，且MN交CC₁點N，

在正△ABC中，AM⊥BC，

又∵平面ABC⊥平面BB₁C₁C，

平面ABC∩平面BB₁C₁C=BC，

∴AM⊥平面BB₁C₁C，

∵MN平面BB₁C₁C，

∴MN⊥AM。

∵AM∩B₁M=M，

∴MN⊥平面AMB₁，∴MN⊥AB₁。

∵在Rt△B₁BM與Rt△MCN中，

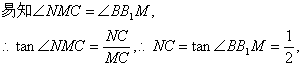
即N為C₁C四等分點（靠近點C）。  ……………………6分

   （2）過點M作ME⊥AB₁，垂足為R，連結EN，

由（1）知MN⊥平面AMB₁，

∴EN⊥AB₁，

∴∠MEN為二面角M―AB₁―N的平面角。

∵正三棱柱ABC―A₁B₁C₁，BB₁=BC=2，

解法2：（1）以點M為原點，建立如圖所示的空間直角坐標系，

∴N點是C₁C的四等分點（靠近點C）。  ………………6分

   （2）∵AM⊥BC，平面ABC⊥平面BB₁C₁C，

且平面ABC∩平面BB₁C₁C=BC，

∴AM⊥平面BB₁C₁C，

∵MN平面BB₁C₁ C，∴AM⊥MN，

∵MN⊥AB₁，∴MN⊥平面AMB₁，