
【題目】(題文)如圖在三棱錐![]() 中,
中, ![]() 分別為棱
分別為棱![]() 的中點,已知
的中點,已知![]() ,
,

求證:(1)直線![]() 平面
平面![]() ;
;
(2)平面![]()
![]() 平面
平面![]() .
.
科目:高中數學 來源: 題型:
【題目】2017年“十一”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如圖的頻率分布直方圖.
,后得到如圖的頻率分布直方圖.

(1)求這40輛小型車輛車速的眾數和中位數的估計值;
(2)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛恰有一輛的概率.
的車輛恰有一輛的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
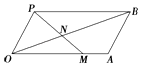
【題目】如圖所示,四邊形OABP是平行四邊形,過點P的直線與射線OA,OB分別相交于點M,N,若 ![]() ,
, ![]() .
. 
(1)把y用x表示出來(即求y=f(x)的解析式);
(2)設數列{an}的首項a1=1,前n項和Sn滿足Sn=f(Sn﹣1)(n≥2且n∈N*),求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海域的東西方向上分別有A,B兩個觀測點(如圖),它們相距![]() 海里.現有一艘輪船在D點發出求救信號,經探測得知D點位于A點北偏東45°,B點北偏西60°,這時,位于B點南偏西60°且與B點相距
海里.現有一艘輪船在D點發出求救信號,經探測得知D點位于A點北偏東45°,B點北偏西60°,這時,位于B點南偏西60°且與B點相距![]() 海里的C點有一救援船,其航行速度為30海里/小時.
海里的C點有一救援船,其航行速度為30海里/小時.

(1)求B點到D點的距離BD;
(2)若命令C處的救援船立即前往D點營救,求該救援船到達D點需要的時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各射擊一次,擊中目標的概率分別是 ![]() 和
和 ![]() .假設兩人射擊是否擊中目標,相互之間沒有影響;每人各次射擊是否擊中目標,相互之間也沒有影響.
.假設兩人射擊是否擊中目標,相互之間沒有影響;每人各次射擊是否擊中目標,相互之間也沒有影響.
(1)求甲射擊4次,至少1次未擊中目標的概率;
(2)求兩人各射擊4次,甲恰好擊中目標2次且乙恰好擊中目標3次的概率;
(3)假設某人連續2次未擊中目標,則停止射擊.問:乙恰好射擊5次后,被中止射擊的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比數列.
(Ⅰ)求{an}的通項公式an與前n項和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差數列,求數列{
(k<0),若{bn}是等差數列,求數列{![]() }的前n項和Tn.
}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲,乙兩個靶,某射手向甲靶射擊一次,命中的概率是 ![]() ,向乙靶射擊兩次,每次命中的概率是
,向乙靶射擊兩次,每次命中的概率是 ![]() ,若該射手每次射擊的結果相互獨立,則該射手完成以上三次射擊恰好命中一次的概率是( )
,若該射手每次射擊的結果相互獨立,則該射手完成以上三次射擊恰好命中一次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)設不等式2x-1>m(x2-1)對滿足|m|≤2的一切實數m的取值都成立,求x的取值范圍;
(2)是否存在m使得不等式2x-1>m(x2-1)對滿足|x|≤2的一切實數x的取值都成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com