
【題目】若數列![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() (
(![]() )中
)中![]() (
(![]() )且對任意的
)且對任意的![]()
![]() 恒成立,則稱數列
恒成立,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(Ⅰ)若數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 為“
為“![]() 數列”,寫出所有可能的
數列”,寫出所有可能的![]() ,
, ![]() ;
;
(Ⅱ)若“![]() 數列”
數列”![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() 中,
中, ![]() ,
, ![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)設![]() 為給定的偶數,對所有可能的“
為給定的偶數,對所有可能的“![]() 數列”
數列”![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() ,
,
記![]() ,其中
,其中![]() 表示
表示![]() ,
, ![]() ,…,
,…, ![]() 這
這![]() 個數中最大的數,求
個數中最大的數,求![]() 的最小值.
的最小值.
【答案】(1) ![]() ,
, ![]() 或
或![]() (2)最大值為
(2)最大值為![]() (3)
(3)![]()
【解析】試題分析:(Ⅰ)直接根據“![]() 數列”的定義,討論列舉法即可求出
數列”的定義,討論列舉法即可求出![]() ,
, ![]() ;(Ⅱ)
;(Ⅱ) ![]() 可得
可得![]() ,解得:
,解得: ![]() ,故
,故![]() ,另外,任意的
,另外,任意的![]() ,
, ![]() ,故數列
,故數列![]() 為“
為“![]() 數列”,此時
數列”,此時![]() ,即
,即![]() 符合題意;(Ⅲ)利用放縮法
符合題意;(Ⅲ)利用放縮法![]() ,即可得結論.
,即可得結論.
試題解析::(Ⅰ) ![]() ,
, ![]() 或
或![]()
(Ⅱ)![]() 的最大值為
的最大值為![]() ,理由如下
,理由如下
一方面,注意到: ![]()
對任意的![]() ,令
,令![]() ,則
,則![]() 且
且![]() (
(![]() ),故
),故![]() 對任意的
對任意的![]() 恒成立.
恒成立.
當![]() ,
, ![]() 時,注意到
時,注意到![]() ,得
,得
![]() (
(![]() )
)
此時
![]()
即![]() ,解得:
,解得: ![]() ,故
,故![]() 另一方面,取
另一方面,取![]() (
(![]() ),則對任意的
),則對任意的![]() ,
, ![]() ,故數列
,故數列![]() 為“
為“![]() 數列”,此時
數列”,此時![]() ,即
,即![]() 符合題意.
符合題意.
綜上, ![]() 的最大值為65.
的最大值為65.
(Ⅲ)![]() 的最小值為
的最小值為![]() ,證明如下:
,證明如下:
當![]() (
(![]() ,
, ![]() )時,
)時,
一方面:
由(★)式, ![]() ,
,
![]() .
.
此時有:
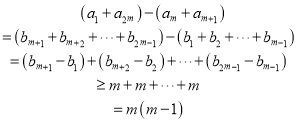
故![]()
另一方面,當![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 時,
時, ![]()
取![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,且
,且
![]()
![]()
此時![]() .
.
綜上, ![]() 的最小值為
的最小值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 內,點
內,點 ![]() 在曲線
在曲線![]() :
:![]() ,(
,(![]() 為參數,
為參數,![]() )上運動,以
)上運動,以![]() 為極軸建立極坐標系.直線
為極軸建立極坐標系.直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 的標準方程和直線
的標準方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 在曲線
在曲線![]() 上移動,求
上移動,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的圖象關于y軸對稱,并且是[0,+∞)上的減函數,若f(lgx)>f(1),則實數x的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據以往的經驗,某工程施工期間的將數量X(單位:mm)對工期的影響如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延誤天數Y | 0 | 2 | 6 | 10 |
歷年氣象資料表明,該工程施工期間降水量X小于300,700,900的概率分別為0.3,0.7,0.9,求:
(1)工期延誤天數Y的均值與方差;
(2)在降水量X至少是300的條件下,工期延誤不超過6天的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了了解某地區電視觀眾對某體育節目的收視情況,隨機抽取了100名觀眾進行調查,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成下面2×2列聯表,并據此資料你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為X,若每次抽取的結果是相互獨立的,求X的分布列,期望E(X)和方差D(X)
P( K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,AD=6,PA⊥底面ABCD,E是PD上的動點.若CE∥平面PAB,則三棱錐C﹣ABE的體積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com