
【題目】某地要建造一個邊長為2(單位:![]() )的正方形市民休閑公園
)的正方形市民休閑公園![]() ,將其中的區域
,將其中的區域![]() 開挖成一個池塘,如圖建立平面直角坐標系后,點
開挖成一個池塘,如圖建立平面直角坐標系后,點![]() 的坐標為
的坐標為![]() ,曲線
,曲線![]() 是函數
是函數![]() 圖像的一部分,過邊
圖像的一部分,過邊![]() 上一點
上一點![]() 在區域
在區域![]() 內作一次函數
內作一次函數![]() (
(![]() )的圖像,與線段
)的圖像,與線段![]() 交于點
交于點![]() (點
(點![]() 不與點
不與點![]() 重合),且線段
重合),且線段![]() 與曲線
與曲線![]() 有且只有一個公共點
有且只有一個公共點![]() ,四邊形
,四邊形![]() 為綠化風景區.
為綠化風景區.
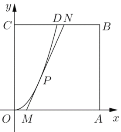
(1)求證:![]() ;
;
(2)設點![]() 的橫坐標為
的橫坐標為![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 兩點的坐標;
兩點的坐標;
②將四邊形![]() 的面積
的面積![]() 表示成關于
表示成關于![]() 的函數
的函數![]() ,并求
,并求![]() 的最大值.
的最大值.
【答案】(1)見解析(2)①M(![]() ,0),N(
,0),N(![]() ,2)②S=4﹣(t
,2)②S=4﹣(t![]() ),其中0<t<1,S的最大值是4
),其中0<t<1,S的最大值是4![]() .
.
【解析】
(1)根據函數y=ax2過點D,求出解析式y=2x2;
由![]() 消去y,利用△=0證明結論成立;
消去y,利用△=0證明結論成立;
(2)①寫出點P的坐標(t,2t2),代入直線MN的方程,用t表示出直線方程,
利用直線方程求出M、N的坐標;
②將四邊形MABN的面積S表示成關于t的函數S(t),
利用基本不等式即可求出S的最大值.
(1)函數y=ax2過點D(1,2),
代入計算得a=2,
∴y=2x2;
由![]() ,消去y得2x2﹣kx﹣b=0,
,消去y得2x2﹣kx﹣b=0,
由線段MN與曲線OD有且只有一個公共點P,
得△=(﹣k)2﹣4×2×b=0,
解得b![]() ;
;
(2)設點P的橫坐標為t,則0<t<1,
∴點P(t,2t2);
①直線MN的方程為y=kx+b,
即y=kx![]() 過點P,
過點P,
∴kt![]() 2t2,
2t2,
解得k=4t;
y=4tx﹣2t2
令y=0,解得x![]() ,∴M(
,∴M(![]() ,0);
,0);
令y=2,解得x![]() ,∴N(
,∴N(![]() ,2);
,2);
②將四邊形MABN的面積S表示成關于t的函數為
S=S(t)=2×2![]() 2×[
2×[![]() (
(![]() )]=4﹣(t
)]=4﹣(t![]() ),其中0<t<1;
),其中0<t<1;
由t![]() 2
2![]() ,當且僅當t
,當且僅當t![]() ,即t
,即t![]() 時“=”成立,
時“=”成立,
所以S≤4![]() ;即S的最大值是4
;即S的最大值是4![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
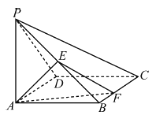
(1)若![]() 為線段
為線段![]() 上的動點,證明:平面
上的動點,證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() ,
,![]() ,
,![]() 上的動點(不含
上的動點(不含![]() ,
,![]() ),
),![]() ,三棱錐
,三棱錐![]() 的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對任意正整數![]() ,若存在數列
,若存在數列![]() ,滿足
,滿足![]() ,其中
,其中![]() ,則稱數列
,則稱數列![]() 為正整數
為正整數![]() 的生成數列,記為
的生成數列,記為![]() .
.
(1)寫出2018的生成數列![]() ;
;
(2)求證:對任意正整數![]() ,存在唯一的生成數列
,存在唯一的生成數列![]() ;
;
(3)求生成數列![]() 的所有項的和.
的所有項的和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別為雙曲線
分別為雙曲線![]()
![]()
![]() 的左、右焦點,點P是以
的左、右焦點,點P是以![]() 為直徑的圓與C在第一象限內的交點,若線段
為直徑的圓與C在第一象限內的交點,若線段![]() 的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別為雙曲線
分別為雙曲線![]()
![]()
![]() 的左、右焦點,點P是以
的左、右焦點,點P是以![]() 為直徑的圓與C在第一象限內的交點,若線段
為直徑的圓與C在第一象限內的交點,若線段![]() 的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“移動支付、高鐵、網購、共享單車”被稱為中國的“新四大發明”.為了幫助50歲以上的中老年人更快地適應“移動支付”,某機構通過網絡組織50歲以上的中老年人學習移動支付相關知識.學習結束后,每人都進行限時答卷,得分都在![]() 內.在這些答卷(有大量答卷)中,隨機抽出
內.在這些答卷(有大量答卷)中,隨機抽出![]() 份,統計得分繪出頻率分布直方圖如圖.
份,統計得分繪出頻率分布直方圖如圖.
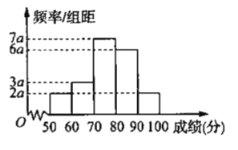
(1)求出圖中![]() 的值,并求樣本中,答卷成績在
的值,并求樣本中,答卷成績在![]() 上的人數;
上的人數;
(2)以樣本的頻率為概率,從參加這次答卷的人群中,隨機抽取![]() 名,記成績在
名,記成績在![]() 分以上(含
分以上(含![]() 分)的人數為
分)的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在地上有同樣大小的 5 塊積木,一堆 2 個,一堆 3 個,要把積木一塊一塊的全部放到某個盒子里,每次 只能取出其中一堆最上面的一塊,則不同的取法有______種(用數字作答).
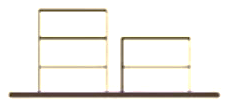
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為平行四邊形,點O為對角線BD的中點,點E,F分別為棱PC,PD的中點,已知PA⊥AB,PA⊥AD.
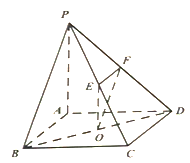
(1)求證:直線PB∥平面OEF;
(2)求證:平面OEF⊥平面ABCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年1月6日,中國物流與采購聯合會正式發布了中國倉儲指數,中國倉儲指數是反映倉儲行業經營和國內市場主要商品供求狀況與變化趨勢的一套指數體系,如圖所示的折線圖是2019年甲企業和乙企業的倉儲指數走勢情況.根據該折線圖,下列結論中不正確的是( )
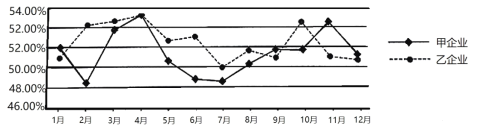
A.2019年1月至4月甲企業的倉儲指數比乙企業的倉儲指數波動大
B.甲企業2019年的年平均倉儲指數明顯低于乙企業2019年的年平均倉儲指數
C.兩企業2019年的最大倉儲指數都出現在4月份
D.2019年7月至9月乙企業的倉儲指數的增幅高于甲企業
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com