
【題目】如圖,三棱柱![]() 的各棱長均相等,
的各棱長均相等, ![]() 底面
底面![]() ,E,F分別為棱
,E,F分別為棱![]() 的中點.
的中點.
(1)過![]() 作平面α,使得直線BE//平面α,若平面α與直線
作平面α,使得直線BE//平面α,若平面α與直線![]() 交于點H,指出點H所在的位置,并說明理由;
交于點H,指出點H所在的位置,并說明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)由直線![]() 平面
平面![]() ,利用線面平行的判定定理可得直線
,利用線面平行的判定定理可得直線![]() 直線
直線![]() ,又
,又![]() 直線
直線![]() ,可得四邊形
,可得四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() ,即
,即![]() 點為
點為![]() 的中點;(2)取
的中點;(2)取![]() 的中點
的中點![]() ,由于
,由于![]() 兩兩互相垂直,所以可以
兩兩互相垂直,所以可以![]() 為軸建立如空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面
為軸建立如空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面![]() 與平面
與平面![]() 的一個法向量,根據空間向量夾角余弦公式,可得結果.
的一個法向量,根據空間向量夾角余弦公式,可得結果.
試題解析:(1)如圖所示,平面FHA1即為平面α,H點為線段BB1的中點.
理由如下:
因為直線BE//平面α,平面α∩平面AB1=A1H,直線BE平面AB1,
所以直線BE//直線A1H,又A1E//直線BH,
所以四邊形BEA1H是平行四邊形,則BH= A1E![]() ,
,
即H點為BB1的中點.
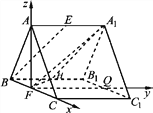
(2)如圖,取B1C1的中點Q,顯然FC,FQ,FA兩兩互相垂直,建立如圖所示的空間直角坐標系F-xyz如圖所示.
不妨設棱長為2,則H(-1,1,0),A1(0,2, ![]() ),
),
則![]() ,
, ![]() ,
,
設面FHA1的法向量![]() ,
,
則由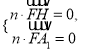 得
得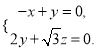
令![]() ,得
,得![]() .
.
取平面BFH的一個法向量![]() ,
,
于是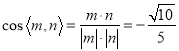 .
.
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
【方法點晴】本題主要考查線面平行的證明以及利用空間向量求二面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


科目:高中數學 來源: 題型:
【題目】某超市計劃銷售某種食品,現邀甲、乙兩個商家進場試銷5天.兩個商家提供的返利方案如下:甲商家每天固定返利60元,且每賣出一件食品商家再返利2元;乙商家無固定返利,賣出30件以內(含30件)的食品,每件食品商家返利4元,超出30件的部分每件返利6元.經統計,兩個商家的試銷情況莖葉圖如下:
甲 | 乙 | |||||||
9 | 8 | 9 | 2 | 8 | 8 | |||
2 | 2 | 3 | 2 | 1 | 1 | |||
(1)現從甲商家試銷的5天中抽取兩天,求這兩天的銷售量都小于30的概率;
(2)超市擬在甲、乙兩個商家中選擇一家長期銷售,如果僅從日平均返利額的角度考慮,請利用所學的統計學知識為超市作出選擇,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在對人們的休閑方式的一次調查中,共調查了110人,其中女性50人,男性60人.女性中有30人主要的休閑方式是看電視,另外20人主要的休閑方式是運動;男性中有20人主要的休閑方式是看電視,另外40人主要的休閑方式是運動.
(1)根據以上數據建立一個2×2列聯表;
(2)判斷性別與休閑方式是否有關系.
下面臨界值表供參考:
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(參考公式:K2=![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班“數學興趣小組”對函數y=﹣x2+2|x|+1的圖象和性質進行了探究,探究過程如下,請補充完整.
(1)自變量x的取值范圍是全體實數,x與y的幾組對應值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,畫出了函數圖象的一部分,請畫出該函數圖象的另一部分.
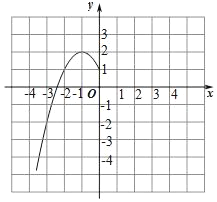
(3)觀察函數圖象,寫出兩條函數的性質.
(4)進一步探究函數圖象發現:
①方程﹣x2+2|x|+1=0有 個實數根;
②關于x的方程﹣x2+2|x|+1=a有4個實數根時,a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一張坐標紙上一已作出圓![]() 及點
及點![]() ,折疊此紙片,使
,折疊此紙片,使![]() 與圓周上某點
與圓周上某點![]() 重合,每次折疊都會留下折痕,設折痕與直線
重合,每次折疊都會留下折痕,設折痕與直線![]() 的交點為
的交點為![]() ,令點
,令點![]() 的軌跡為
的軌跡為![]() .
.
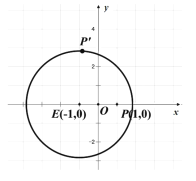
(1)求軌跡![]() 的方程;
的方程;
(2)若直線![]() 與軌跡
與軌跡![]() 交于兩個不同的點
交于兩個不同的點![]() ,且直線
,且直線![]() 與以
與以![]() 為直徑的圓相切,若
為直徑的圓相切,若![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班數學興趣小組對函數![]() 的圖象和性質將進行了探究,探究過程如下,請補充完整.
的圖象和性質將進行了探究,探究過程如下,請補充完整.

(1)自變量![]() 的取值范圍是除
的取值范圍是除![]() 外的全體實數,
外的全體實數,![]() 與
與![]() 的幾組對應值列表如下:
的幾組對應值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根據上表數據,在如圖所示的平面直角坐標系中描點并畫出了函數圖象的一部分,請畫出該函數圖象的另一部分;
(3)觀察函數圖象,寫出一條函數性質;
(4)進一步探究函數圖象發現:
①函數圖象與![]() 軸交點情況是________,所以對應方程
軸交點情況是________,所以對應方程![]() 的實數根的情況是________;
的實數根的情況是________;
②方程![]() 有_______個實數根;
有_______個實數根;
③關于![]() 的方程
的方程![]() 有
有![]() 個實數根,
個實數根,![]() 的取值范圍是________.
的取值范圍是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖,90后從事互聯網行業崗位分布條形圖,則下列結論中不正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.


A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的![]()
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com