
【題目】如圖,在直三棱柱![]() 中,
中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 的中點.
的中點.
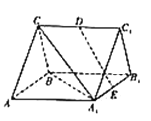
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見證明;(2) ![]()
【解析】
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,據題設可得四邊形
,據題設可得四邊形![]() 是平行四邊形,根據線面平行的證明定理即可得證;
是平行四邊形,根據線面平行的證明定理即可得證;
(2)延長![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,根據題設條件可證明
,根據題設條件可證明![]() ,
,![]() ,
,![]() 兩兩垂直,因而以O為原點,以
兩兩垂直,因而以O為原點,以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標系,寫出各個點的坐標,即可求得平面
軸的正方向建立空間直角坐標系,寫出各個點的坐標,即可求得平面![]() 的法向量為,根據直線與平面夾角的正弦值為直線與平面法向量夾角的余弦值即可得解
的法向量為,根據直線與平面夾角的正弦值為直線與平面法向量夾角的余弦值即可得解
(1)證明:設點![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,
,
∵![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,
∴![]() ,且
,且![]() .
.
又在平行四邊形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,
∴![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:如圖,延長![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
則由(1)![]() 及
及![]() 知
知![]() ,
,
且![]() 是
是![]() 的中點,
的中點,
∵![]() 是正三角形,
是正三角形,
∴![]() .
.
又在直三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,故
,故![]() ,
,
所以![]() ,
,![]() ,
,![]() 兩兩垂直.
兩兩垂直.
如圖,分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標系
軸的正方向建立空間直角坐標系![]() ,
,
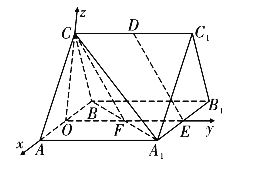
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則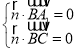 ,即
,即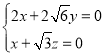 ,解得
,解得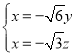 ,
,
∴可取![]() .
.
設直線![]() 與平面
與平面![]() 的所成角為
的所成角為![]() ,
,
則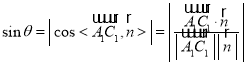
![]() ,
,
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】農機公司出售收割機,一臺收割機的使用壽命為五年,在農機公司購買收割機時可以一次性額外訂購買若干次維修服務,費用為每次100元,每次維修時公司維修人員均上門服務,實際上門服務時還需支付維修人員的餐飲費50元/次;若實際維修次數少于購買的維修次數,則未提供服務的訂購費用退還50%;如果維修次數超過了購買的次數,農機公司不再提供服務,收割機的維修只能到私人維修店,每次維修費用為400元,無須支付餐飲費;--位農機手在購買收割機時,需決策一次性購買多少次維修服務.
為此,他擬范收集整理出一臺收割機在五年使用期內維修次數及相應的頻率如下表:

(1)如果農機手在購買收割機時購買了6次維修,在使用期內實際維修的次數為5次,這位農機手的花費總費用是多少?如果實際維修的次數是8次,農機手的花費總費用又是多少?
(2)農機手購買了一臺收制機,試在購買維修次數為6次和7次的兩個數據中,根據使用期內維修時花費的總費用期望值,幫助農機手進行決策.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再把橫坐標縮短到原來的
個單位長度,再把橫坐標縮短到原來的![]() 倍(縱坐標不變)得到函數
倍(縱坐標不變)得到函數![]() 的圖像,則下列說法正確的是( )
的圖像,則下列說法正確的是( )
A. 函數![]() 的最小正周期為
的最小正周期為![]()
B. 函數![]() 在區間
在區間![]() 上單調遞增
上單調遞增
C. 函數![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]()
D. ![]() 是函數
是函數![]() 的一條對稱軸
的一條對稱軸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 前n項和為
前n項和為![]() ,且
,且![]() 其中m為實常數,
其中m為實常數,![]() 且
且![]() .
.
(1)求證:![]() 是等比數列;
是等比數列;
(2)若數列![]() 的公比滿足
的公比滿足![]() 且
且![]() ,
,![]() ,求證:數列
,求證:數列![]() 是等差數列,并求
是等差數列,并求![]() 的通項公式;
的通項公式;
(3)若![]() 時,設
時,設![]() ,求數列
,求數列![]() 的前n和
的前n和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個結論:
①在回歸分析模型中,殘差平方和越大,說明模型的擬合效果越好;
②某學校有男教師60名、女教師40名,為了解教師的體育愛好情況,在全體教師中抽取20名調查,則宜采用的抽樣方法是分層抽樣;
③線性相關系數![]() 越大,兩個變量的線性相關性越弱;反之,線性相關性越強;
越大,兩個變量的線性相關性越弱;反之,線性相關性越強;
④在回歸方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 增加0.5個單位.
增加0.5個單位.
其中正確的結論是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,點O是四邊形ABCD的中心,關于直線A1O,下列說法正確的是( )
A. A1O∥DCB. A1O⊥BCC. A1O∥平面BCDD. A1O⊥平面ABD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com