
【題目】已知點![]() ,圓
,圓![]() :
:![]() ,過點
,過點![]() 的動直線
的動直線![]() 與圓
與圓![]() 交于A,B兩點,線段AB的中點為M,O為坐標原點.
交于A,B兩點,線段AB的中點為M,O為坐標原點.
求M的軌跡方程;
當|OP|=|OM|時,求![]()
![]() 的方程及
的方程及![]() 的面積
的面積
【答案】(1)(x﹣1)2+(y﹣3)2=2(2)![]()
【解析】分析:(1)由圓![]() 的方程求出圓心坐標和半徑,設出
的方程求出圓心坐標和半徑,設出![]() 的坐標,由
的坐標,由![]() 與
與![]() 數量積等于
數量積等于![]() 可得
可得![]() 的軌跡方程;(2)設
的軌跡方程;(2)設![]() 的軌跡的圓心為
的軌跡的圓心為![]() ,由
,由![]() 得到
得到![]() ,求出
,求出![]() 所在直線的斜率,由直線方程的點斜式得到
所在直線的斜率,由直線方程的點斜式得到![]() 所在直線方程,由點到直線的距離公式求出
所在直線方程,由點到直線的距離公式求出![]() 到直線
到直線![]() 的距離,再由弦心距、圓的半徑及弦長間的關系求出
的距離,再由弦心距、圓的半徑及弦長間的關系求出![]() 的長度,代入三角形面積公式得結論.
的長度,代入三角形面積公式得結論.
詳解:(1)由圓C:x2+y2﹣8y=0,得x2+(y﹣4)2=16,
∴圓C的圓心坐標為(0,4),半徑為4.
設M(x,y),則![]() ,
,![]() .
.
由題意可得:![]() .
.
即x(2﹣x)+(y﹣4)(2﹣y)=0.整理得:(x﹣1)2+(y﹣3)2=2.
由于點P在圓C內部,
∴M的軌跡方程是(x﹣1)2+(y﹣3)2=2.
(2)由(1)知M的軌跡是以點N(1,3)為圓心,![]() 為半徑的圓,
為半徑的圓,
由于|OP|=|OM|,故O在線段PM的垂直平分線上,
又P在圓N上,從而ON⊥PM.
∵kON=3,∴直線l的斜率為﹣![]() .
.
∴直線PM的方程為![]() ,即x+3y﹣8=0.
,即x+3y﹣8=0.
則O到直線l的距離為![]() .
.
又N到l的距離為![]() ,
,
∴|PM|=![]() =
=![]() .
.
∴![]() .
.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知e為自然對數的底數,設函數f(x)=(ex﹣1)(x﹣1)k(k=1,2),則( )
A.當k=1時,f(x)在x=1處取得極小值
B.當k=1時,f(x)在x=1處取得極大值
C.當k=2時,f(x)在x=1處取得極小值
D.當k=2時,f(x)在x=1處取得極大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點P(0,﹣1)是橢圓C1: ![]() +
+ ![]() =1(a>b>0)的一個頂點,C1的長軸是圓C2:x2+y2=4的直徑,l1 , l2是過點P且互相垂直的兩條直線,其中l1交圓C2于A、B兩點,l2交橢圓C1于另一點D.
=1(a>b>0)的一個頂點,C1的長軸是圓C2:x2+y2=4的直徑,l1 , l2是過點P且互相垂直的兩條直線,其中l1交圓C2于A、B兩點,l2交橢圓C1于另一點D. 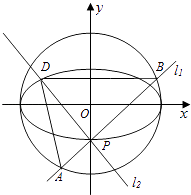
(1)求橢圓C1的方程;
(2)求△ABD面積的最大值時直線l1的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子里裝有7張卡片,其中有紅色卡片4張,編號分別為1,2,3,4; 白色卡片3張,編號分別為2,3,4.從盒子中任取4張卡片 (假設取到任何一張卡片的可能性相同).
(1)求取出的4張卡片中,含有編號為3的卡片的概率.
(2)在取出的4張卡片中,紅色卡片編號的最大值設為X,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】節日前夕,小李在家門前的樹上掛了兩串彩燈,這兩串彩燈的第一次閃亮相互獨立,且都在通電后的4秒內任一時刻等可能發生,然后每串彩燈以4秒為間隔閃亮,那么這兩串彩燈同時通電后,它們第一次閃亮的時候相差不超過2秒的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com