【題目】（本小題滿分16分）已知
是虛數， 
是實數．
（1）求
為何值時， 
有最小值，并求出|
的最小值；
（2）設
，求證： 
為純虛數．
【答案】（1）
（2）見解析
【解析】試題分析：（1）設
，化簡
，利用
是虛數
為實數，解得
的軌跡方程，利用幾何意義即可的結果；（2）根據（1）的結論化簡
即可得結論.
試題解析：（1）設
，則
所以， 
，又
可得
表示點
到點
的距離，所以
最小值為
解方程組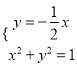
并結合圖形得
（2）
又
，所以
為純虛數
【 思路點晴】本題主要考查的是復數的乘法、除法運算和復數模的概念及復數的幾何性質，屬于難題題．解題時一定要注意
和運算的準確性，否則很容易出現錯誤．解本題的關鍵是先利用復數的模長公式列方程解出
的值，然后根據復數的乘法、除法的運算法則和
的性質化簡
+
，最后再根據復數的幾何意義求出
的范圍. 
； 
， 
， 
， 
（
）．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知數列
為等差數列， 
，公差
，且其中的三項
成等比.
（1）求數列
的通項公式以及它的前n項和
；
（2）若數列
滿足
，
為數列的前
項和，求；
（3）在（2）的條件下，若不等式
（
）恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，六面體ABCDHEFG中，四邊形ABCD為菱形，AE，BF，CG，DH都垂直于平面ABCD.若DA＝DH＝DB＝4，AE＝CG＝3。
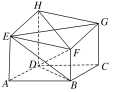
(1)求證：EG⊥DF；
(2)求BE與平面EFGH所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業生產A、B兩種產品，根據市場調查，A產品的利潤與投資成正比，其關系如圖1，B產品的利潤與投資的算術平方根成正比，其關系如圖2(注：單位是萬元).
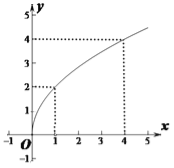
圖1圖2
（1）分別將A、B兩種產品的利潤表示為投資的函數，寫出它們的函數關系式；
（2）現企業有20萬元資金全部投入A、B兩種產品的生產，問：怎樣分配這20萬元資金，能使獲得的利潤最大，其最大利潤是多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小明準備利用暑假時間去旅游，媽媽為小明提供四個景點，九寨溝、泰山、長白山、武夷山．小明決定用所學的數學知識制定一個方案來決定去哪個景點：（如圖）曲線
和直線
交于點
．以
為起點，再從曲線
上任取兩個點分別為終點得到兩個向量，記這兩個向量的數量積為
．若
去九寨溝；若
去泰山；若
去長白山； 
去武夷山．
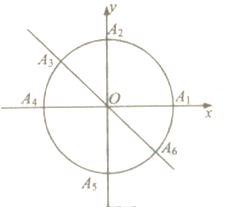
（1）若從
這六個點中任取兩個點分別為終點得到兩個向量，分別求小明去九寨溝的概率和不去泰山的概率；
（2）按上述方案，小明在曲線
上取點
作為向量的終點，則小明決定去武夷山．點
在曲線
上運動，若點
的坐標為
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知M(x0，y0)是橢圓C：
＋
＝1上的任一點，從原點O向圓M：(x－x0)2＋(y－y0)2＝2作兩條切線，分別交橢圓于點P，Q.
(1)若直線OP，OQ的斜率存在，并記為k1，k2，求證：k1k2為定值；
(2)試問|OP|2＋|OQ|2是否為定值？若是，求出該值；若不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是等差數列，從a1，a2，a3，a4，a5，a6，a7中取走任意四項，則剩下三項構成等差數列的概率為( )
A. 
B. 
C．1或 D．1或
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2＋y2＝4，直線l：x＋y＝2.以O為極點，x軸的正半軸為極軸，取相同的單位長度建立極坐標系．
(1)將圓C和直線l的方程化為極坐標方程；
(2)P是l上的點，射線OP交圓C于點R，又點Q在OP上且滿足|OQ|·|OP|＝|OR|2，當點P在l上移動時，求點Q軌跡的極坐標方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
