日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
O、A、B、C為空間四邊形四個頂點，點M、N分別是邊OA、BC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示向量
MN
為（　　）
A、
1
2
（
a
+
c
-
b
）
B、
1
2
（
a
+
b
-
c
）
C、
1
2
（
c
+
b
-
a
）
D、
1
2
（
a
+
b
+
c
）
分析：由題意，O、A、B、C為空間四邊形四個頂點，點M、N分別是邊OA、BC的中點，由用向量的加法法則可以得出
MN
=
MA
+
AB
+
BN
，根據圖形用
a
，
b
，
c
表示出再對照四個選項得出正確答案
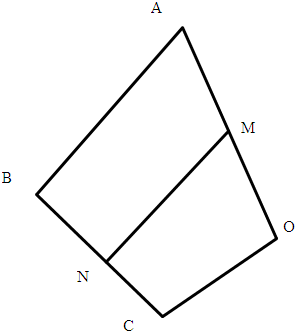解答：精英家教網解：如圖
MN
=
MA
+
AB
+
BN

又點M、N分別是邊OA、BC的中點
∴
MN
=
MA
+
AB
+
BN

=
1
2
OA
+
AB
+
BN

=
1
2
OA
+
OB
-
OA
+
1
2
BC

=
1
2
OA
+
OB
-
OA
+
1
2
×(
OC
-
OB
)
=-
1
2
OA
+
1
2
OB
+
1
2
OC

又
OA
=
a
，
OB
=
b
，
OC
=
c
，
∴
MN
=
1
2
（
c
+
b
-
a
）
故選C
點評：本題考查向量的加減運算及其幾何意義，解題的關鍵是作出圖象由向量的線性運算規則用三個向量表示出向量
MN
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

有以下命題：
①如果向量
a
，
b
與任何向量不能構成空間向量的一組基底，那么
a
，
b
的關系是不共線；
②O，A，B，C為空間四點，且向量
OA
，
OB
，
OC
不構成空間的一個基底，那么點O，A，B，C一定共面；
③已知向量
a
，
b
，
c
是空間的一個基底，則向量
a
+
b
，
a
-
b
，
c
，也是空間的一個基底．
其中正確的命題是（　　）
A、①②B、①③C、②③D、①②③

查看答案和解析>>

科目：高中數學 來源： 題型：

有4個命題：
①O，A，B，C為空間四點，且
OA
，
OB
，
OC
不構成空間的一個基底，那么點O，A，B，C一定共面
②若
a
與
b
共線，
b
與
c
共線，則
a
與
c
共線
③若
p
與
a
，
b
共面，則
p
=x
a
+y
b

④若
MP
=x
MA
+y
MB
，則P，M，A，B共面
其中，真命題的個數是（　　）

查看答案和解析>>

科目：高中數學 來源： 題型：

已知點O、A、B、C為空間不共面的四點，且向量
a
=
OA
+
OB
+
OC
，向量
b
=
OA
+
OB
-
OC
，則與
a
、
b
不能構成空間基底的向量是（　　）
A、
OA
B、
OB
C、
OC
D、
OA
或
OB

查看答案和解析>>

科目：高中數學 來源：2013屆福建省高二上學期期末考試理科數學試卷A 題型：選擇題

O、A、B、C為空間四個點，又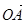、、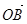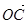為空間的一個基底，則（  ）

A.  O、A、B、C四點共線               B.  O、A、B、C四點共面

C.  O、A、B、C四點中任三點不共線     D.  O、A、B、C四點不共面

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 色呦呦入口 | 国产综合精品一区二区三区 | 久久精品99国产精品亚洲最刺激 | 亚洲一级电影 | 国产a久久精品一区二区三区 | 国产精品天堂 | 欧美一区二区大片 | 日本三级网 | 国产三区二区一区 | 亚洲视频在线播放 | 精品久久久久久久久久 | 久久久久综合网 | 午夜小影院 | 亚洲综人网 | 国产精品一区二区在线 | 成人精品网站在线观看 | 亚洲成人自拍 | 老师的朋友2 | 久久免费精品视频 | 美日韩免费视频 | 狠狠色狠狠色综合网 | 韩日精品| 国产一级中文字幕 | 人人草在线观看视频 | 国产一区二区三区在线免费 | 在线日本看片免费人成视久网 | 亚洲精品乱 | 视频二区| 国产精品久久久久免费视频 | 日韩在线欧美 | 黄色大片网站 | 国产精品自拍一区 | 在线亚洲一区二区 | 国产一区免费 | 自拍小电影 | 奇米影| 久久久免费 | 狠狠色综合欧美激情 | 日韩高清国产一区在线 | 久久精品久久久久久 | 国产亲子乱弄免费视频 |