
分析 設t=f(x)-log2x,則f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f(x)的解析式,由二分法分析可得h(x)的零點所在的區間為(1,2),結合函數的零點與方程的根的關系,即可得答案.
解答 解:根據題意,對任意的x∈(0,+∞),都有f[f(x)-log2x]=3,
又由f(x)是定義在(0,+∞)上的單調函數,
則f(x)-log2x為定值,
設t=f(x)-log2x,則f(x)=log2x+t,
又由f(t)=3,即log2t+t=3,
解可得,t=2;
則f(x)=log2x+2,f′(x)=$\frac{1}{ln2•x}$,
將f(x)=log2x+2,f′(x)=$\frac{1}{xln2}$代入f(x)-f′(x)=2,
可得log2x+2-$\frac{1}{xln2}$=2,
即log2x-$\frac{1}{xln2}$=0,
令h(x)=log2x-$\frac{1}{xln2}$,
分析易得h(1)=$\frac{1}{ln2}$<0,h(2)=1-$\frac{1}{2ln2}$>0,
則h(x)=log2x-$\frac{1}{xln2}$的零點在(1,2)之間,
則方程log2x-$\frac{1}{xln2}$=0,即f(x)-f′(x)=2的根在(1,2)上,
故答案為:1.
點評 本題考查二分法求函數的零點與函數零點與方程根的關系的應用,關鍵點和難點是求出f(x)的解析式.


科目:高中數學 來源: 題型:選擇題
| A. | 2lg5 | B. | 0 | C. | -1 | D. | -2lg5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 圖象關于$x=\frac{π}{3}$對稱 | |
| B. | 圖象關于$(\frac{2π}{3},0)$對稱 | |
| C. | 在$[\frac{2π}{3},\frac{8π}{3}]$上單調遞減 | |
| D. | 單調遞增區間是$[2kπ-\frac{4π}{3},2kπ+\frac{2π}{3}](k∈Z)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
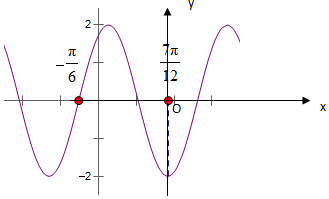 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的圖象如圖所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | -1 | C. | -1或3 | D. | 0 或 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com