
已知函數 ,
, .
.
(1)求函數 的最小正周期和單調遞減區間;
的最小正周期和單調遞減區間;
(2)已知 中的三個內角
中的三個內角 所對的邊分別為
所對的邊分別為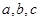 ,若銳角
,若銳角 滿足
滿足 ,且
,且 ,
, ,求
,求 的面積.
的面積.
(1)最小正周期為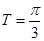 ,單調遞減區間是
,單調遞減區間是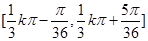 ,
,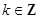 ;
;
(2)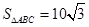 .
.
解析試題分析:(1)首先應用三角函數公式,化簡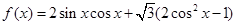 得到
得到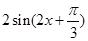 ,從而得到
,從而得到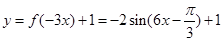
其最小正周期為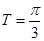 ,由復合函數的單調性,由
,由復合函數的單調性,由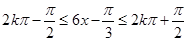 解得,
解得,
函數 的單調遞減區間是
的單調遞減區間是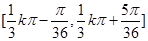 ,
,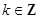 ;
;
(2)由已知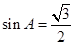 ,根據
,根據 ,求得
,求得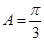 .
.
由正弦定理可得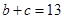 ;
;
應用余弦定理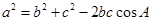 得:
得: ,
,
求得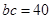 ,應用三角形面積計算公式即可得解.
,應用三角形面積計算公式即可得解.
解得本題,巧妙地利用“整體觀”,確定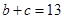 及
及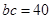 ,簡化了解題過程.
,簡化了解題過程.
試題解析:(1)
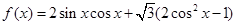
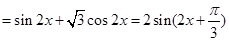 2分
2分
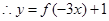 的最小正周期為
的最小正周期為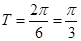 3分
3分
由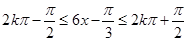 得:
得: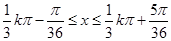 ,
,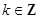 ,
, 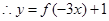 的單調遞減區間是
的單調遞減區間是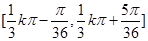 ,
,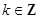 6分
6分
(2)∵ ,∴
,∴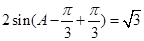 ,∴
,∴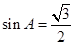 7分
7分
∵ ,∴
,∴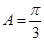 .由正弦定理得:
.由正弦定理得: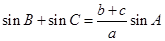 ,
,
即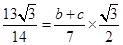 ,∴
,∴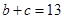 9分
9分
由余弦定理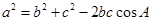 得:
得: ,
,
即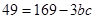 ,∴
,∴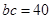 11分
11分
∴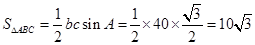 12分
12分
考點:三角函數式的化簡,三角函數的性質,正弦、余弦定理的應用,三角形面積公式.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
如圖,經過村莊A有兩條夾角為60°的公路AB,AC,根據規劃擬在兩條公路之間的區域內建一工廠P,分別在兩條公路邊上建兩個倉庫M、N (異于村莊A),要求PM=PN=MN=2(單位:千米).如何設計, 可以使得工廠產生的噪聲對居民的影響最小(即工廠與村莊的距離最遠).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 中,
中, 的對邊分別為
的對邊分別為 且
且 .
.
(1)判斷△ 的形狀,并求
的形狀,并求 的取值范圍;
的取值范圍;
(2)如圖,三角形 的頂點
的頂點 分別在
分別在 上運動,
上運動, ,若直線
,若直線 直線
直線 ,且相交于點
,且相交于點 ,求
,求 間距離的取值范圍.
間距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某人沿一條折線段組成的小路前進,從 到
到 ,方位角(從正北方向順時針轉到
,方位角(從正北方向順時針轉到 方向所成的角)是
方向所成的角)是 ,距離是3km;從
,距離是3km;從 到
到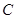 ,方位角是110°,距離是3km;從
,方位角是110°,距離是3km;從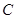 到
到 ,方位角是140°,距離是(
,方位角是140°,距離是( )km.試畫出大致示意圖,并計算出從A到D的方位角和距離(結果保留根號).
)km.試畫出大致示意圖,并計算出從A到D的方位角和距離(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com