
分析 根據f(x)定義域為全體實數,可得mx2-2x+1>0,方程x2+(m-3)x+m=0的一根在(0,1)內,另一根在(1,2)內,利用根的分布建立不等式求解m的范圍.要求s∨t為真命題,先求解出s∧t為假命題時,實數m的取值范圍,即可得到s∨t為真命題實數m的取值范圍.
解答 解:由題意,函數f(x)=ln(mx2-2x+1)的定義域為全體實數;
∴mx2-2x+1>0對一切實數x恒成立,
可得:$\left\{\begin{array}{l}{m>0}\\{△<0}\end{array}\right.$,即$\left\{\begin{array}{l}{m>0}\\{4-4m<0}\end{array}\right.$,
解得:m>1.
令g(x)=x2+(m-3)x+m=0的一根在(0,1)內,另一根在(1,2)內.
可得:$\left\{\begin{array}{l}{g(0)>0}\\{g(1)<0}\\{g(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{m>0}\\{2m<2}\\{3m>2}\end{array}\right.$,
解得:$\frac{2}{3}<m<1$.
當s∧t為假命題時:則s為假,且t也為假.
即$\left\{\begin{array}{l}{m≤1}\\{1≤m或m≤\frac{2}{3}}\end{array}\right.$,
∴得m的范圍是(-∞,$\frac{2}{3}$]∪{1}
故得s∨t為真命題,實數m的取值范圍為($\frac{2}{3},1$)∪(1,+∞).
點評 本題考查的知識點是二次函數的性質,其中根據方程的根與零點零點的關系,根的分布建立不等式是解答本題的關鍵.要求s∨t為真命題時m的范圍,可以通過求解出s∧t為假命題來解決.屬于中檔題.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | -5 | B. | 0 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
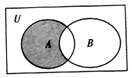 若全集U、集合A、集合B及其關系用韋恩圖表示如圖所示,則圖中陰影表示的集合為( )
若全集U、集合A、集合B及其關系用韋恩圖表示如圖所示,則圖中陰影表示的集合為( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 任何事件的概率總是在(0,1]之間 | |
| B. | 頻率是客觀存在的,與試驗次數無關 | |
| C. | 隨著試驗次數的增加,事件發生的頻率一般會穩定于概率 | |
| D. | 概率是隨機的,在試驗前不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com