
【題目】已知以 ![]() 為一條漸近線的雙曲線C的右焦點為
為一條漸近線的雙曲線C的右焦點為 ![]() .
.
(1)求該雙曲線C的標準方程;
(2)若斜率為2的直線l在雙曲線C上截得的弦長為 ![]() ,求l的方程.
,求l的方程.
【答案】
(1)解:由拋物線的焦點在x軸上,設雙曲線的標準方程: ![]() (a>0,b>0),
(a>0,b>0),
由c= ![]() ,漸近線方程:y=±
,漸近線方程:y=± ![]() x,
x,
∴ ![]() =
= ![]() ,即
,即 ![]() ,即2a2=3b2,
,即2a2=3b2,
由c2=a2﹣b2=5,解得:a2=3,b2=2,
∴雙曲線C的標準方程 ![]()
(2)解:設l:y=2x+m,與雙曲線的交點為:M(x1,y1),N(x2,y2).
則  ,整理得:10x2+12mx+3m2+6=0,
,整理得:10x2+12mx+3m2+6=0,
由韋達定理可知: ![]()
∴ ![]() ,
,
解得, ![]() .
.
∴l的方程 ![]()
【解析】(1)設雙曲線的標準方程: ![]() (a>0,b>0),由c=
(a>0,b>0),由c= ![]() ,漸近線方程:y=±
,漸近線方程:y=± ![]() x,
x, ![]() ,由c2=a2﹣b2=5,即可求得a和b的值,求得雙曲線的標準方程;(2)設l:y=2x+m,代入雙曲線方程,利用韋達定理及弦長公式即可求得m的值,即可求得l的方程.
,由c2=a2﹣b2=5,即可求得a和b的值,求得雙曲線的標準方程;(2)設l:y=2x+m,代入雙曲線方程,利用韋達定理及弦長公式即可求得m的值,即可求得l的方程.


科目:高中數學 來源: 題型:
【題目】三棱錐ABCD中,BC=DC=AB=AD= ![]() ,BD=2,平面ABD⊥平面BCD,O為BD的中點,P、Q分別為線段AO,BC上的動點,且AP=CQ,求三棱錐PQCO體積的最大值.
,BD=2,平面ABD⊥平面BCD,O為BD的中點,P、Q分別為線段AO,BC上的動點,且AP=CQ,求三棱錐PQCO體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(ax﹣1)(x+b),如果不等式f(x)>0的解集是(﹣1,3),則不等式f(﹣x)<0的解集是( )
A.(﹣∞,﹣1)∪(3,+∞)
B.(﹣3,1)
C.(﹣∞,﹣3)∪(1,+∞)
D.(﹣1,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=4x+a2x+b,
(1)若f(0)=1,f(﹣1)=﹣ ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)由(1)當0≤x≤2時,求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正方體ABCD﹣A1B1C1D1中,AA1 , AB,CC1的中點分別為E,F,G,則EF與A1G所成的角為( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD,底面ABCD為邊長為2對的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分別是BC,PC的中點. 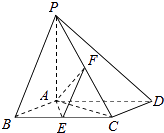
(1)判定AE與PD是否垂直,并說明理由;
(2)若PA=2,求二面角E﹣AF﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到周期y=sin(2x+ ![]() )的圖象,只需把函數y=sin(2x﹣
)的圖象,只需把函數y=sin(2x﹣ ![]() )的圖象( )
)的圖象( )
A.向左平移 ![]() 個單位長度
個單位長度
B.向右平移 ![]() 個單位長度
個單位長度
C.向左平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= ![]() AD=2,點G為AC的中點.
AD=2,點G為AC的中點. 
(Ⅰ)求證:平面BAE⊥平面DCE;
(Ⅱ)求三棱錐B﹣AEG的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com