
【題目】先將函數y=f(x)的圖象向左平移 ![]() 個單位,然后再將所得圖象上所有點的縱坐標不變,橫坐標伸長到原來的2倍,最后再將所得圖象向上平移1個單位,得到函數y=sinx的圖象.
個單位,然后再將所得圖象上所有點的縱坐標不變,橫坐標伸長到原來的2倍,最后再將所得圖象向上平移1個單位,得到函數y=sinx的圖象.
(Ⅰ)求函數y=f(x)的解析式;
(Ⅱ)若函數y=g(x)與y=f(x)的圖象關于點M( ![]() ,2)對稱,求函數y=g(x)在[0,
,2)對稱,求函數y=g(x)在[0, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
【答案】解:(Ⅰ)由題意可得,把函數y=sinx的圖象向下平移1個單位得y=sinx﹣1的圖象,
然后再將y=sinx﹣1圖象上所有點的縱坐標不變,橫坐標縮短到原來的 ![]() 倍,得到y=sin2x﹣1的圖象,
倍,得到y=sin2x﹣1的圖象,
最后將函數y=sin2x﹣1的圖象向右平移 ![]() 個單位得y=sin2(x﹣
個單位得y=sin2(x﹣ ![]() )﹣1的圖象,
)﹣1的圖象,
所以函數y=f(x)的表達式是y=sin(2x﹣ ![]() )﹣1.
)﹣1.
(Ⅱ)設函數y=f(x)=sin(2x﹣ ![]() )﹣1圖象任意一點為P(m,n),點P(m,n)關于點M(
)﹣1圖象任意一點為P(m,n),點P(m,n)關于點M( ![]() ,2)對稱點為Q(x,y),
,2)對稱點為Q(x,y),
由于函數y=g(x)與y=f(x)的圖象關于點M( ![]() ,2)對稱,點Q(x,y)是函數y=g(x)圖象上的點.
,2)對稱,點Q(x,y)是函數y=g(x)圖象上的點.
由中點坐標公式可得m+x= ![]() 且 n+y=4,即 m=
且 n+y=4,即 m= ![]() ﹣x且 n=4﹣y.
﹣x且 n=4﹣y.
由點P(m,n)在函數 y=sin(2x﹣ ![]() )﹣1的圖象上,可得n=sin(2m﹣
)﹣1的圖象上,可得n=sin(2m﹣ ![]() )﹣1,即有4﹣y=sin[2(
)﹣1,即有4﹣y=sin[2( ![]() ﹣x)﹣
﹣x)﹣ ![]() )]﹣1,
)]﹣1,
化簡得y=sin(2x﹣ ![]() )+5,所以函數y=g(x)的解析式為y=sin(2x﹣
)+5,所以函數y=g(x)的解析式為y=sin(2x﹣ ![]() )+5.
)+5.
由于x∈[0, ![]() ],所以y=g(x)=sin(2x﹣
],所以y=g(x)=sin(2x﹣ ![]() )+5,根據2x﹣
)+5,根據2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],y=sin(2x﹣
],y=sin(2x﹣ ![]() )+5∈[4,5+
)+5∈[4,5+ ![]() ],
],
函數y=g(x)在[0, ![]() ]的最小值和最大值分別為4和5+
]的最小值和最大值分別為4和5+ ![]()
【解析】(Ⅰ)由條件利用函數y=Asin(ωx+φ)的圖象變換規律,得出結論.(Ⅱ)由條件利用兩個函數的圖象關于某個點對稱的性質,正弦函數的定義域和值域,求得函數y=g(x)在[0, ![]() ]的最小值和最大值.
]的最小值和最大值.
【考點精析】解答此題的關鍵在于理解函數y=Asin(ωx+φ)的圖象變換的相關知識,掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三個向量,其中
是同一平面上的三個向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐標.
的坐標.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 與2
與2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 與
與 ![]() 的夾角θ
的夾角θ
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,OAB是一塊半徑為1,圓心角為 ![]() 的扇形空地.現決定在此空地上修建一個矩形的花壇CDEF,其中動點C在扇形的弧
的扇形空地.現決定在此空地上修建一個矩形的花壇CDEF,其中動點C在扇形的弧 ![]() 上,記∠COA=θ.
上,記∠COA=θ.
(Ⅰ)寫出矩形CDEF的面積S與角θ之間的函數關系式;
(Ⅱ)當角θ取何值時,矩形CDEF的面積最大?并求出這個最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】園林管理處擬在公園某區域規劃建設一半徑為![]() 米圓心角為
米圓心角為![]() (弧度)的扇形景觀水池,其中
(弧度)的扇形景觀水池,其中![]() 為扇形
為扇形![]() 的圓心,同時緊貼水池周邊建一圈理想的無寬度步道,要求總預算費用不超過
的圓心,同時緊貼水池周邊建一圈理想的無寬度步道,要求總預算費用不超過![]() 萬元,水池造價為每平方米
萬元,水池造價為每平方米![]() 元,步道造價為每米
元,步道造價為每米![]() 元.
元.
(1)當![]() 和
和![]() 分別為多少時,可使廣場面積最大,并求出最大值;
分別為多少時,可使廣場面積最大,并求出最大值;
(2)若要求步道長為![]() 米,則可設計出水池最大面積是多少.
米,則可設計出水池最大面積是多少.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosx,cosx),
=(cosx,cosx), ![]() =(sinx,﹣cosx),記函數f(x)=2
=(sinx,﹣cosx),記函數f(x)=2 ![]()
![]() +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函數f(x)的最小正周期及函數f(x)的圖象的對稱中心的坐標;
(Ⅱ)若α∈(0, ![]() ),且f(
),且f( ![]() )=
)= ![]() ,求cos2α的值.
,求cos2α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點P的坐標為(x﹣3,y﹣2).
(1)在一個盒子中,放有標號為1,2,3的三張卡片,現在從盒子中隨機取出一張卡片,記下標號后把卡片放回盒中,再從盒子中隨機取出一張卡片記下標號,記先后兩次抽取卡片的標號分別為x、y,求點P在第二象限的概率;
(2)若利用計算機隨機在區間[0,3]上先后取兩個數分別記為x、y,求點P在第三象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD是平行四邊形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中點..
,且M是BD的中點.. 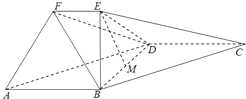
(1)求證:EM∥平面ADF;
(2)求直線DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com