
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
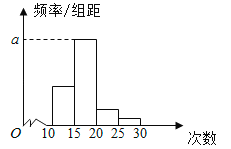
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合計 |
| 1 |
(1)求出表中![]() ,
,![]() 及圖中
及圖中![]() 的值;
的值;
(2)若該校高三學生人數有500人,試估計該校高三學生參加社區服務的次數在區間![]() 內的人數;
內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至多一人參加社區服務次數在區間![]() 內的概率.
內的概率.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)150;(3)
;(2)150;(3)![]() .
.
【解析】
(1)根據頻率,頻數和樣本容量之間的關系即頻率等于頻數除以樣本容量,寫出算式,求出式子中的字母的值;
(2)該校高三學生有500人,分組![]() 內的頻率是030,可估計該校高三學生參加社區服務的次數在此區間內的人數;
內的頻率是030,可估計該校高三學生參加社區服務的次數在此區間內的人數;
(3)設在區間![]() 內的人為
內的人為![]() ,
,![]() ,
,![]() ,
,![]() ,在區間
,在區間![]() 內的人為
內的人為![]() ,
,![]() ,寫出任選2人的所有基本事件,利用對立事件求得答案.
,寫出任選2人的所有基本事件,利用對立事件求得答案.
(1)由分組![]() 內的頻數是15,頻率是0.30知,
內的頻數是15,頻率是0.30知,![]() ,∴
,∴![]() .
.
∵頻數之和為50,∴![]() ,
,![]() ,
,![]() .
.
∵![]() 是對應分組
是對應分組![]() 的頻率與組距的商,∴
的頻率與組距的商,∴![]() ;
;
故![]() ,
,![]() ,
,![]() ;
;
(2)因為該校高三學生有500人,分組![]() 內的頻率是0.30,
內的頻率是0.30,
∴估計該校高三學生參加社區服務的次數在此區間內的人數為150人.
(3)這個樣本參加社區服務的次數不少于20次的學生共有![]() 人,
人,
設在區間![]() 內的人為
內的人為![]() ,
,![]() ,
,![]() ,
,![]() ,在區間
,在區間![]() 內的人為
內的人為![]() ,
,![]() .
.
則任選2人共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 15種情況,而兩人都在
15種情況,而兩人都在![]() 內只能是
內只能是![]() 一種,
一種,
∴所求概率為![]() .
.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】某大學餐飲中心為了了解新生的飲食習慣,在全校一年級學生中進行了抽樣調查,調查結果如下表所示:
喜歡甜食 | 不喜歡甜食 | 合計 | |
南方學生 | 60 | 20 | 80 |
北方學生 | 10 | 10 | 20 |
合計 | 70 | 30 | 100 |
附: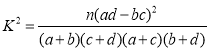
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(1)根據表中數據,問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差異”;
(2)已知在被調查的北方學生中有5名數學系的學生,其中2名喜歡甜品,現在從這5名學生中隨機抽取3人,求至多有1人喜歡甜品的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究一種昆蟲的產卵數![]() 和溫度
和溫度![]() 是否有關,現收集了7組觀測數據列于下表中,并作出了如圖的散點圖.
是否有關,現收集了7組觀測數據列于下表中,并作出了如圖的散點圖.
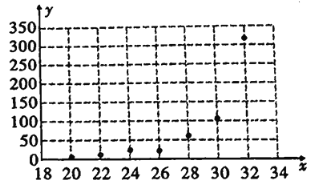
溫度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
產卵數 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79.4 | 3.58 | 112 | 11.6 | 2340 | 35.72 |
其中![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作為該昆蟲的產卵數
哪一個更適宜作為該昆蟲的產卵數![]() 與溫度
與溫度![]() 的回歸方程類型?(給出判斷即可,不必說明理由).
的回歸方程類型?(給出判斷即可,不必說明理由).
(2)根據表中數據,建立![]() 關于
關于![]() 的回歸方程;(保留兩位有效數字)
的回歸方程;(保留兩位有效數字)
(3)根據![]() 關于
關于![]() 的回歸方程,估計溫度為33℃時的產卵數.
的回歸方程,估計溫度為33℃時的產卵數.
(參考數據:![]() )
)
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為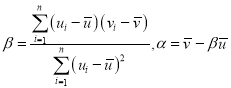 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解學生使用手機的情況,分別在高一和高二兩個年級各隨機抽取了100名學生進行調查.下面是根據調查結果繪制的學生日均使用手機時間的頻數分布表和頻率分布直方圖,將使用手機時間不低于80分鐘的學生稱為“手機迷”.
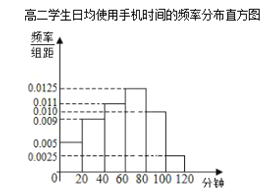
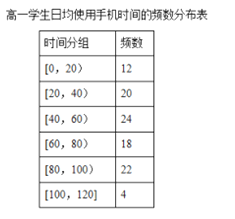
(I)將頻率視為概率,估計哪個年級的學生是“手機迷”的概率大?請說明理由.
(II)在高二的抽查中,已知隨機抽到的女生共有55名,其中10名為“手機迷”.根據已知條件完成下面的2×2列聯表,并據此資料你有多大的把握認為“手機迷”與性別有關?
非手機迷 | 手機迷 | 合計 | |
男 | |||
女 | |||
合計 |
附:隨機變量![]() (其中
(其中![]() 為樣本總量).
為樣本總量).
參考數據 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期,西安公交公司分別推出支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,![]() 表示活動推出的天數,
表示活動推出的天數,![]() 表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
![]()
根據以上數據,繪制了散點圖.
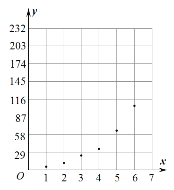
(1)根據散點圖判斷,在推廣期內,![]() 與
與![]() (
(![]() 均為大于零的常數),哪一個適宜作為掃碼支付的人次
均為大于零的常數),哪一個適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型?(給出判斷即可,不必說明理由);
的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表1中的數據,建立![]() 與
與![]() 的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
(3)推廣期結束后,車隊對乘客的支付方式進行統計,結果如下表:
![]()
西安公交六公司車隊為緩解周邊居民出行壓力,以![]() 萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為
萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為![]() 萬元.已知該線路公交車票價為
萬元.已知該線路公交車票價為![]() 元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受
元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受![]() 折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有
折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠.預計該車隊每輛車每個月有
折優惠.預計該車隊每輛車每個月有![]() 萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要
萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要![]() (
(![]() )年才能開始盈利,求
)年才能開始盈利,求![]() 的值.
的值.
參考數據:
|
|
|
|
|
|
|
|
|
|
其中其中![]() ,
,![]() ,
,
參考公式:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: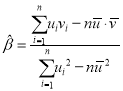 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
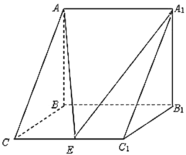
【題目】如圖,三棱柱![]() 中,
中,![]() 側面
側面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com