
【題目】某種產品的廣告費支出x與銷售額y(單位:萬元)之間有如表對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求廣告費支出x與銷售額y回歸直線方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 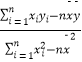 ,
, ![]()
(2)在已有的五組數據中任意抽取兩組,求至少有一組數據其預測值與實際值之差的絕對值不超過5的概率.
【答案】
(1)解:由題意得 ![]() ,
, ![]() ,
,  ,
,
![]() ,
,
所求回歸直線方程為 ![]()
(2)解:基本事件:(30,40),(30,60),(30,50),(30,70),
(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10個
兩組數據其預測值與實際值之差的絕對值都超過5:(60,50)
所以至少有一組數據其預測值與實際值之差的絕對值不超過5的概率為 ![]()
【解析】(1)首先求出x,y的平均數,利用最小二乘法做出線性回歸方程的系數,根據樣本中心點滿足線性回歸方程,代入已知數據求出a的值,寫出線性回歸方程.(2)分別求出在已有的五組數據中任意抽取兩組的情況總數,及至少有一組數據其預測值與實際值之差的絕對值不超過5的情況數,代入古典概型概率計算公式,可得答案.


科目:高中數學 來源: 題型:
【題目】已知X和Y是兩個分類變量,由公式K2= ![]() 算出K2的觀測值k約為7.822根據下面的臨界值表可推斷( )
算出K2的觀測值k約為7.822根據下面的臨界值表可推斷( )
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.推斷“分類變量X和Y沒有關系”犯錯誤的概率上界為0.010
B.推斷“分類變量X和Y有關系”犯錯誤的概率上界為0.010
C.有至少99%的把握認為分類變量X和Y沒有關系
D.有至多99%的把握認為分類變量X和Y有關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=|lnx|,若函數g(x)=f(x)﹣ax在區間(0,3]上有三個零點,則實數a的取值范圍是( )
A.(0, ![]() )
)
B.( ![]() ,e)
,e)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于三次函數f(x)=ax3+bx2+cx+d(a≠0),給出定義:設f′(x)是函數y=f(x)的導數,f′′(x)是f′(x)的導數,若方程f′′(x)有實數解x0 , 則稱點(x0 , f(x0))為函數y=f(x)的“拐點”.某同學經過探究發現:任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.設函數f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,請你根據這一發現,計算f(
,請你根據這一發現,計算f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+
,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+ ![]() 的取值范圍是( )
的取值范圍是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某創業團隊擬生產![]() 兩種產品,根據市場預測,
兩種產品,根據市場預測, ![]() 產品的利潤與投資額成正比(如圖1),
產品的利潤與投資額成正比(如圖1),![]() 產品的利潤與投資額的算術平方根成正比(如圖2).(注: 利潤與投資額的單位均為萬元)
產品的利潤與投資額的算術平方根成正比(如圖2).(注: 利潤與投資額的單位均為萬元)

(1)分別將![]() 兩種產品的利潤
兩種產品的利潤![]() 、
、![]() 表示為投資額
表示為投資額![]() 的函數;
的函數;
(2)該團隊已籌集到10 萬元資金,并打算全部投入![]() 兩種產品的生產,問:當
兩種產品的生產,問:當![]() 產品的投資額為多少萬元時,生產
產品的投資額為多少萬元時,生產![]() 兩種產品能獲得最大利潤,最大利潤為多少?
兩種產品能獲得最大利潤,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
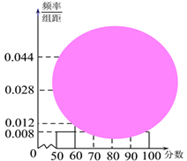
【題目】某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如下圖:
![]() 求分數在
求分數在![]() 的頻率及全班人數;
的頻率及全班人數;
![]() 求分數在
求分數在![]() 之間的頻數,并計算頻率分布直方圖中
之間的頻數,并計算頻率分布直方圖中![]() 間矩形的高;
間矩形的高;
![]() 若要從分數在
若要從分數在![]() 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在![]() 之間的概率.
之間的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列各組中兩個函數是否為同一函數.
(1)f(x)=x2+2x﹣1,g(x)=t2+2t﹣1;
(2)f(x)=![]() , g(x)=x+1;
, g(x)=x+1;
(3)f(x)=![]()
![]() , g(x)=
, g(x)=![]() ;
;
(4)f(x)=|3﹣x|+1,g(x)=![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com