
數列![]() ,
,![]() (
(![]() )由下列條件確定:①
)由下列條件確定:①![]() ;②當
;②當![]() 時,
時,![]() 與
與![]() 滿足:當
滿足:當![]() 時,
時,![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,寫出
,寫出![]() ,并求數列
,并求數列![]() 的通項公式;
的通項公式;
(Ⅱ)在數列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),試用
),試用![]() 表示
表示![]()
![]() ;
;
(Ⅲ)在(Ⅰ)的條件下,設數列![]()
![]() 滿足
滿足![]() ,
,![]() ,
,
![]() (其中
(其中![]() 為給定的不小于2的整數),求證:當
為給定的不小于2的整數),求證:當![]() 時,恒有
時,恒有![]() .
.
(Ⅰ)解:因為![]() ,所以
,所以![]() ,
,![]() .
.
因為![]() ,所以
,所以![]() ,
,![]() .
.
因為![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() . …………………………………… 2分
. …………………………………… 2分
由此猜想,當![]() 時,
時,![]() ,則
,則![]() ,
,![]() .… 3分
.… 3分
下面用數學歸納法證明:
①當![]() 時,已證成立.
時,已證成立.
②假設當![]() (
(![]() ,且
,且![]() )猜想成立,
)猜想成立,
即![]() ,
,![]() ,
,![]() .
.
當![]() 時,由
時,由![]() ,
, ![]() 得
得![]() ,則
,則![]() ,
,![]() .
.
綜上所述,猜想成立.
所以![]() .
.
故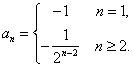 . ……………………………………………… 6分
. ……………………………………………… 6分
(Ⅱ)解:當![]() 時,假設
時,假設![]() ,根據已知條件則有
,根據已知條件則有![]() ,
,
與![]() 矛盾,因此
矛盾,因此![]() 不成立, …………… 7分
不成立, …………… 7分
所以有![]() ,從而有
,從而有![]() ,所以
,所以![]() .
.
當![]() 時,
時,![]() ,
,![]() ,
,
所以![]() ; …………………… 8分
; …………………… 8分
當![]() 時,總有
時,總有![]() 成立.
成立.
又![]() ,
,
所以數列![]() (
(![]() )是首項為
)是首項為![]() ,公比為
,公比為![]() 的等比數列,
的等比數列, ![]() ,
,![]() ,
,
又因為![]() ,所以
,所以![]() . …………………………… 10分
. …………………………… 10分
(Ⅲ)證明:由題意得![]()
![]() .
.
因為![]() ,所以
,所以![]() .
.
所以數列![]() 是單調遞增數列. …………………………………… 11分
是單調遞增數列. …………………………………… 11分
因此要證![]() ,只須證
,只須證![]() .
.
由![]() ,則
,則![]() <
<![]() ,即
,即![]() .…… 12分
.…… 12分
因此![]()
![]() .
.
所以![]() .
.
故當![]() ,恒有
,恒有![]() . …………………………………………………14分
. …………………………………………………14分


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源:2011-2012學年北京市朝陽區高三上學期期末考試理科數學 題型:解答題
(本題滿分14分)
數列 ,
, (
( )由下列條件確定:①
)由下列條件確定:① ;②當
;②當 時,
時, 與
與 滿足:當
滿足:當 時,
時, ,
, ;當
;當 時,
時, ,
, .
.
(Ⅰ)若 ,
, ,寫出
,寫出 ,并求數列
,并求數列 的通項公式;
的通項公式;
(Ⅱ)在數列 中,若
中,若 (
(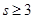 ,且
,且 ),試用
),試用 表示
表示
 ;
;
(Ⅲ)在(Ⅰ)的條件下,設數列
 滿足
滿足 ,
, ,
,
 (其中
(其中 為給定的不小于2的整數),求證:當
為給定的不小于2的整數),求證:當 時,恒有
時,恒有 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
數列![]() ,
,![]() (
(![]() )由下列條件確定:①
)由下列條件確定:①![]() ;②當
;②當![]() 時,
時,![]() 與
與![]() 滿足:當
滿足:當![]() 時,
時,![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,寫出
,寫出![]() ,并求數列
,并求數列![]() 的通項公式;
的通項公式;
(Ⅱ)在數列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),試用
),試用![]() 表示
表示![]()
![]() ;
;
(Ⅲ)在(Ⅰ)的條件下,設數列![]()
![]() 滿足
滿足![]() ,
,![]() ,
,
![]() (其中
(其中![]() 為給定的不小于2的整數),求證:當
為給定的不小于2的整數),求證:當![]() 時,恒有
時,恒有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
數列![]() ,
,![]() (
(![]() )由下列條件確定:①
)由下列條件確定:①![]() ;②當
;②當![]() 時,
時,![]() 與
與![]() 滿足:當
滿足:當![]() 時,
時,![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,求
,求![]() ,
,![]() ,
,![]() ,并猜想數列
,并猜想數列![]() 的通項公式(不需要證明);
的通項公式(不需要證明);
(Ⅱ)在數列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),試用
),試用![]() 表示
表示![]() ,
,![]() ;
;
(Ⅲ)在(Ⅰ)的條件下,設數列![]()
![]() 滿足
滿足![]() ,
,![]() ,
,![]() (其中
(其中![]() 為給定的不小于2的整數),求證:當
為給定的不小于2的整數),求證:當![]() 時,恒有
時,恒有![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com