
【題目】已知函數f(x)=log2(16x+k)﹣2x (k∈R)是偶函數.
(1)求k;
(2)若不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求實數m的取值范圍.
]上恒成立,求實數m的取值范圍.
【答案】
(1)解:∵f(x)=log2(16x+k)﹣2x=log2(4x+ ![]() ),
),
∴f(﹣x)=log2(4﹣x+ ![]() )=log2(k4x+4﹣x),
)=log2(k4x+4﹣x),
由f(﹣x)=f(x)恒成立,得k=1
(2)解:∵log2(4x+4﹣x),令t=4x,由x∈[﹣1, ![]() ],
],
∴t∈[ ![]() ,2],
,2],
∵函數y=t+ ![]() 在[
在[ ![]() ,1]上單調遞增,在[1,2]上單調遞減,
,1]上單調遞增,在[1,2]上單調遞減,
∴當t=1時,即x=0時,函數f(x)有最小值f(0)=1,
∴當t= ![]() 時,即x=﹣1時,函數f(x)有最大值f(﹣1)=log2
時,即x=﹣1時,函數f(x)有最大值f(﹣1)=log2 ![]() ,
,
∵m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,
]上恒成立,
∴m﹣1≤1且log2 ![]() ≤2m+log217.
≤2m+log217.
解得﹣1≤m≤2
故m的取值范圍為[﹣1,2]
【解析】(1)由偶函數的定義f(﹣x)=f(x)恒成立可求;(2)不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求出函數f(x)最值即可.
]上恒成立,求出函數f(x)最值即可.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
(1函數f(x)=loga(2x﹣1)﹣1的圖象過定點(1,0);
(2化簡2 ![]() +lg5lg2+(lg2)2﹣lg2的結果為25;
+lg5lg2+(lg2)2﹣lg2的結果為25;
(3若loga ![]() <1,則a的取值范圍是(1,+∞);
<1,則a的取值范圍是(1,+∞);
(4若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),則x+y<0.
其中所有正確命題的序號是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+θ)( A>0,ω>0,|θ|< ![]() )的最小正周期為π,且圖象上有一個最低點為M(
)的最小正周期為π,且圖象上有一個最低點為M( ![]() ,﹣3).
,﹣3).
(1)求f(x)的解析式;
(2)求函數f(x)在[0,π]的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蔬菜基地種植西紅柿,由歷年市場行情得知,從二月一日起的300天內,西紅柿場售價與上市時間的關系如圖一的一條折線表示;西紅柿的種植成本與上市時間的關系如圖二的拋物線段表示. 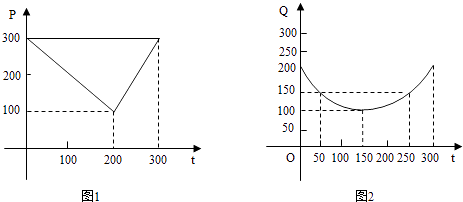
(1)寫出圖一表示的市場售價與時間的函數關系式p=f(t);寫出圖二表示的種植成本與時間的函數關系式Q=g(t);
(2)認定市場售價減去種植成本為純收益,問何時上市的西紅柿純收益最大?(注:市場售價各種植成本的單位:元/102㎏,時間單位:天)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px(p>0)上的一點M的橫坐標為3,焦點為F,且|MF|=4.直線l:y=2x﹣4與拋物線C交于A,B兩點.
(Ⅰ)求拋物線C的方程;
(Ⅱ)若P是x軸上一點,且△PAB的面積等于9,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cosxsin(x﹣ ![]() )+
)+ ![]() .
.
(1)求函數f(x)的對稱軸方程;
(2)若方程sin2x+2|f(x+ ![]() )|﹣m+1=0在x∈[﹣
)|﹣m+1=0在x∈[﹣ ![]() ,
, ![]() ]上有三個實數解,求實數m的取值范圍.
]上有三個實數解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC內的一點.
,AC=3, BC=2,P是△ABC內的一點.
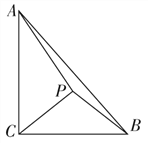
(1)若P是等腰直角三角形PBC的直角頂點,求PA的長;
(2)若∠BPC=![]() ,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com