
分析 (1)由題設知a2=b2+16,$\frac{9}{4{a}^{2}}$+$\frac{75}{4{b}^{2}}$=1,由此能求出橢圓C的標準方程.
(2)由A(-6,0),F(4,0),($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),則得$\overrightarrow{AP}$=($\frac{15}{2}$,$\frac{5\sqrt{3}}{2}$),$\overrightarrow{FP}$=(-$\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$),所以$\overrightarrow{AP}$$•\overrightarrow{FP}$=0,以AF為直徑的圓M必過點P,因此,過P點能引出該圓M的切線,設切線為PQ,交x軸于Q點,又AF的中點為M(-1,0),則顯然PQ⊥PM,由此能求出所求的圖形面積.
解答 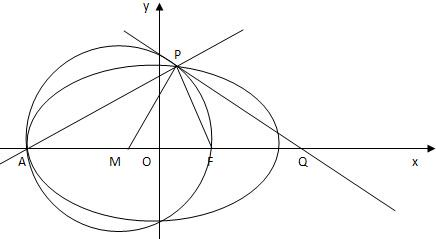 解:(1)由題意a2=b2+16,
解:(1)由題意a2=b2+16,
$\frac{9}{4{a}^{2}}$+$\frac{75}{4{b}^{2}}$=1,
解得b2=20或b2=-15(舍),
由此得a2=36,
所以,所求橢圓C的標準方程為$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}$=1.(6分)
(2)由(1)知A(-6,0),F(4,0),
又($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),則得$\overrightarrow{AP}$=($\frac{15}{2}$,$\frac{5\sqrt{3}}{2}$),$\overrightarrow{FP}$=(-$\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$).
所以$\overrightarrow{AP}$$•\overrightarrow{FP}$=0,即∠APF=90°,△APF是Rt△,
所以,以AF為直徑的圓M必過點P,因此,過P點能引出該圓M的切線,
設切線為PQ,交x軸于Q點,又AF的中點為M(-1,0),則顯然PQ⊥PM,
而kPM=$\sqrt{3}$,所以PQ的斜率為-$\frac{\sqrt{3}}{3}$,
因此,過P點引圓M的切線方程為:y-$\frac{5\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{3}$(x-$\frac{3}{2}$),即x+$\sqrt{3}$y-9=0.
令y=0,則x=9,∴Q(9,0),又M(-1,0),
所以S扇形MPF=$\frac{1}{2}×5×5×\frac{π}{3}$=$\frac{25π}{6}$,
因此,所求的圖形面積是S=S△PQM-S扇形MPF=$\frac{75\sqrt{3}-25π}{6}$.
點評 本題考查直線和圓錐曲線的位置關系,解題時要認真審題,仔細解答,注意合理地進行等價轉化.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,3) | B. | (-1,3) | C. | (3,5) | D. | (-1,5) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
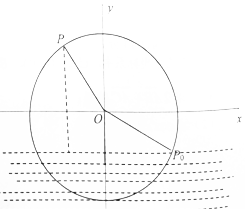 一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉動5圈,如果當水輪上點P從水中浮現時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉動5圈,如果當水輪上點P從水中浮現時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com