
【題目】已知圓![]() ,點
,點![]() 為直線
為直線![]() 上一動點,過點P引圓M的兩條切線,切點分別為A,B.
上一動點,過點P引圓M的兩條切線,切點分別為A,B.
(1)若P的坐標為![]() ,求切線方程;
,求切線方程;
(2)求四邊形PAMB面積的最小值.
【答案】![]()
![]() 和
和![]() ;
;![]()
![]()
【解析】
![]() 由題意知切線的斜率存在,設切線方程為
由題意知切線的斜率存在,設切線方程為![]()
![]() ,由圓心
,由圓心![]() 到直線
到直線![]() 的距離等于半徑求出斜率
的距離等于半徑求出斜率![]() ,代入切線方程即可;
,代入切線方程即可;
![]() 設四邊形PAMB面積為
設四邊形PAMB面積為![]() ,結合題意知,
,結合題意知,![]()
![]() ,求出切線長
,求出切線長![]() 的最小值即可,結合勾股定理知,
的最小值即可,結合勾股定理知,![]() ,即求線段
,即求線段![]() 的最小值,由點
的最小值,由點![]() 為
為![]() ,點
,點![]() 為直線
為直線![]() 上一動點知,當線段
上一動點知,當線段![]() 與直線
與直線![]() 垂直時,
垂直時,![]() 取最小值,利用點到直線的距離公式求出
取最小值,利用點到直線的距離公式求出![]() 的最小值即可.
的最小值即可.
![]() 由題意知切線的斜率存在,設切線方程為
由題意知切線的斜率存在,設切線方程為![]()
![]() ,
,
由點到直線的距離公式可得,點![]() 到直線
到直線![]() 的距離為
的距離為
![]() ,解得
,解得![]() 或
或![]() ,
,
所以所求的切線方程為![]() 和
和![]() ;
;
![]() 設四邊形PAMB面積為
設四邊形PAMB面積為![]() ,因為
,因為![]() 為圓
為圓![]() 的切線,
的切線,
所以![]() ,即
,即![]() ,
,
因為![]() ,所以
,所以![]() ,
,
即當![]() 取最小值時四邊形PAMB面積
取最小值時四邊形PAMB面積![]() 取得最小值,
取得最小值,
因為![]() ,
,
所以當![]() 取最小值時
取最小值時![]() 取最小值,
取最小值,
因為點![]() 為
為![]() ,點
,點![]() 為直線
為直線![]() 上一動點,
上一動點,
所以當線段![]() 與直線
與直線![]() 垂直時,
垂直時,![]() 取最小值,
取最小值,
由點到直線的距離公式可得,
![]() 的最小值為
的最小值為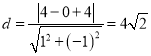 ,
,
此時![]() 取最小值為
取最小值為![]() ,
,
所以四邊形PAMB面積的最小值為![]()
![]() .
.


科目:高中數學 來源: 題型:
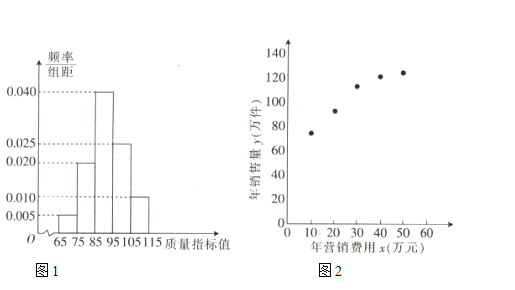
【題目】某企業生產一種產品,從流水線上隨機抽取![]() 件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在
件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損
的為特優品,銷售時劣質品每件虧損![]() 元,優等品每件盈利
元,優等品每件盈利![]() 元,特優品每件盈利
元,特優品每件盈利![]() 元,以這
元,以這![]() 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
(1)求每件產品的平均銷售利潤;
(2)該企業主管部門為了解企業年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對該企業近
(單位:萬件)的影響,對該企業近![]() 年的年營銷費用
年的年營銷費用![]() 和年銷售量
和年銷售量![]() ,
,![]() 數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②用所求的回歸方程估計該企業每年應投入多少營銷費,才能使得該企業的年收益的預報值達到最大?(收益![]() 銷售利潤
銷售利潤![]() 營銷費用,取
營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為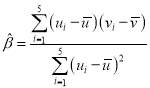 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB//CD,∠ABD=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF.
(Ⅰ)求證:平面ADE⊥平面BDEF;
(Ⅱ)若二面角C![]() BF
BF![]() D的大小為60°,求CF與平面ABCD所成角的正弦值.
D的大小為60°,求CF與平面ABCD所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地自2014年至2019年每年年初統計所得的人口數量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人數(單位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根據表中的數據判斷從2014年到2019年哪個跨年度的人口增長數量最大?并描述該地人口數量的變化趨勢;
(2)研究人員用函數![]() 擬合該地的人口數量,其中
擬合該地的人口數量,其中![]() 的單位是年,2014年年初對應時刻
的單位是年,2014年年初對應時刻![]() ,
,![]() 的單位是千人,經計算可得
的單位是千人,經計算可得![]() ,請解釋
,請解釋![]() 的實際意義.
的實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曲線![]() 的極坐標方程為
的極坐標方程為![]() (常數
(常數![]() ),曲線
),曲線![]() 的參數方程為
的參數方程為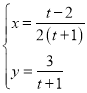 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程和
的直角坐標方程和![]() 的普通方程;
的普通方程;
(2)若曲線![]() ,
,![]() 有兩個不同的公共點,求實數
有兩個不同的公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“初中數學靠練,高中數學靠悟”.總結反思自己已經成為數學學習中不可或缺的一部分,為了了解總結反思對學生數學成績的影響,某校隨機抽取200名學生,抽到不善于總結反思的學生概率是0.6.
(1)完成![]() 列聯表(應適當寫出計算過程);
列聯表(應適當寫出計算過程);
(2)試運用獨立性檢驗的思想方法分析是否有![]() 的把握認為學生的學習成績與善于總結反思有關.
的把握認為學生的學習成績與善于總結反思有關.
統計數據如下表所示:
不善于總結反思 | 善于總結反思 | 合計 | |
學習成績優秀 | 40 | ||
學習成績一般 | 20 | ||
合計 | 200 |
參考公式:![]() 其中
其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省新課改后某校為預測2020屆高三畢業班的本科上線情況,從該校上一屆高三(1)班到高三(5)班隨機抽取50人,得到各班抽取的人數和其中本科上線人數,并將抽取數據制成下面的條形統計圖.
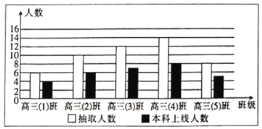
(1)根據條形統計圖,估計本屆高三學生本科上線率.
(2)已知該省甲市2020屆高考考生人數為4萬,假設以(1)中的本科上線率作為甲市每個考生本科上線的概率.
(i)若從甲市隨機抽取10名高三學生,求恰有8名學生達到本科線的概率(結果精確到0.01);
(ii)已知該省乙市2020屆高考考生人數為3.6萬,假設該市每個考生本科上線率均為![]() ,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
可能用到的參考數據:取![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于正整數![]() ,如果
,如果![]() 個整數
個整數![]() 滿足
滿足![]() ,
,
且![]() ,則稱數組
,則稱數組![]() 為
為![]() 的一個“正整數分拆”.記
的一個“正整數分拆”.記![]() 均為偶數的“正整數分拆”的個數為
均為偶數的“正整數分拆”的個數為![]() 均為奇數的“正整數分拆”的個數為
均為奇數的“正整數分拆”的個數為![]() .
.
(Ⅰ)寫出整數4的所有“正整數分拆”;
(Ⅱ)對于給定的整數![]() ,設
,設![]() 是
是![]() 的一個“正整數分拆”,且
的一個“正整數分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)對所有的正整數![]() ,證明:
,證明:![]() ;并求出使得等號成立的
;并求出使得等號成立的![]() 的值.
的值.
(注:對于![]() 的兩個“正整數分拆”
的兩個“正整數分拆”![]() 與
與![]() ,當且僅當
,當且僅當![]() 且
且![]() 時,稱這兩個“正整數分拆”是相同的.)
時,稱這兩個“正整數分拆”是相同的.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com