
已知函數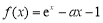 (
(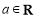 ).
).
(1)求函數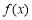 的單調區間;
的單調區間;
(2)函數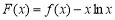 在定義域內是否存在零點?若存在,請指出有幾個零點;若不存在,請說明理由;
在定義域內是否存在零點?若存在,請指出有幾個零點;若不存在,請說明理由;
(3)若 ,當
,當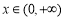 時,不等式
時,不等式 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
(1)當 時,函數
時,函數 的單調增區間為
的單調增區間為 ;當
;當 時,函數
時,函數 的單調增區間為
的單調增區間為 ,單調減區間為
,單調減區間為 ;(2)當
;(2)當 時,函數
時,函數 有兩個不同的零點;當
有兩個不同的零點;當 時,函數
時,函數 有且僅有一個零點;當
有且僅有一個零點;當 時,函數
時,函數 沒有零點;(3)
沒有零點;(3) 的取值范圍是
的取值范圍是 .
.
【解析】
試題分析:(1)首先求導: ,再根據導數的符號確定其單調性.
,再根據導數的符號確定其單調性. 時,函數
時,函數 單調遞增;
單調遞增; 時,函數
時,函數 單調減;(2)首先分離參數.由
單調減;(2)首先分離參數.由 ,得
,得 .令
.令
 (
( ),下面就利用導數研究函數
),下面就利用導數研究函數 性質,然后結合圖象便可得知
性質,然后結合圖象便可得知 的零點的個數;(3)注意
的零點的個數;(3)注意 是一個確定的函數,為了弄清
是一個確定的函數,為了弄清 何時成立,首先弄清
何時成立,首先弄清 與
與 的大小關系,然后利用(1)題的結果即可知道,
的大小關系,然后利用(1)題的結果即可知道,  取何值時
取何值時 在
在 上恒成立.
上恒成立.
(1)由 ,則
,則 .
.
當 時,對
時,對 ,有
,有 ,所以函數
,所以函數 在區間
在區間 上單調遞增;
上單調遞增;
當 時,由
時,由 ,得
,得 ;由
;由 ,得
,得 ,
,
此時函數 的單調增區間為
的單調增區間為 ,單調減區間為
,單調減區間為 .
.
綜上所述,當 時,函數
時,函數 的單調增區間為
的單調增區間為 ;
;
當 時,函數
時,函數 的單調增區間為
的單調增區間為 ,單調減區間為
,單調減區間為 . 4分
. 4分
(2)函數 的定義域為
的定義域為 ,由
,由 ,得
,得 (
( ), 5分
), 5分
令
 (
( ),則
),則
 , 6分
, 6分
由于 ,
, ,可知當
,可知當 ,
, ;當
;當 時,
時, ,
,
故函數 在
在 上單調遞減,在
上單調遞減,在 上單調遞增,故
上單調遞增,故 . 7分
. 7分
又由(1)知當 時,對
時,對 ,有
,有 ,即
,即 ,
,
(隨著 的增長,
的增長, 的增長速度越越快,會超過并遠遠大于
的增長速度越越快,會超過并遠遠大于 的增長速度,而
的增長速度,而 的增長速度則會越越慢.則當
的增長速度則會越越慢.則當 且
且 無限接近于0時,
無限接近于0時, 趨向于正無窮大.)
趨向于正無窮大.)
當 時,函數
時,函數 有兩個不同的零點;
有兩個不同的零點;
當 時,函數
時,函數 有且僅有一個零點;
有且僅有一個零點;
當 時,函數
時,函數 沒有零點. 9分
沒有零點. 9分
(3)由(2)知當 時,
時, ,故對
,故對 ,
,
先分析法證明: ,
, . 10分
. 10分
要證 ,
, ,
,
只需證 ,
,
即證 ,
,
構造函數
 ,則
,則 ,
,
故函數 在
在 單調遞增,所以
單調遞增,所以 ,則
,則 成立. 12分
成立. 12分
當 時,由(1),
時,由(1), 在
在 單調遞增,則
單調遞增,則 在
在 上恒成立;
上恒成立;
當 時,由(1),函數
時,由(1),函數 在
在 單調遞增,在
單調遞增,在 單調遞減,
單調遞減,
故當 時,
時, ,所以
,所以 ,則不滿足題意.
,則不滿足題意.
所以滿足題意的 的取值范圍是
的取值范圍是 . 14分
. 14分
考點:1、導數及其應用;2、函數的零點;3、導數與不等式.


科目:高中數學 來源:2013-2014學年四川省高三下學期3月月考理科數學試卷(解析版) 題型:選擇題
8. 設函數f(x)在R上可導,其導函數為f ′(x),且函數f(x)在x=﹣2處取得極小值,則函數y=xf ′(x)的圖象可能是( )
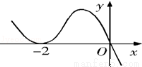
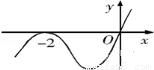
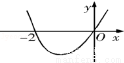
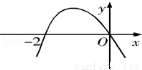
A B C D
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三下學期3月月考文科數學試卷(解析版) 題型:選擇題
一幾何體的三視圖如圖所示,則該幾何體的體積為( )

A.200+9π B.200+18π C.140+9π D.140+18π
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省資陽市高三下學期4月高考模擬考試理科數學試卷(解析版) 題型:解答題
設平面向量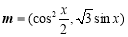 ,
,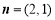 ,函數
,函數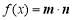 .
.
(1)當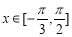 時,求函數
時,求函數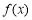 的取值范圍;
的取值范圍;
(2)當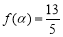 ,且
,且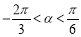 時,求
時,求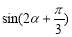 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省資陽市高三下學期4月高考模擬考試理科數學試卷(解析版) 題型:選擇題
設P是雙曲線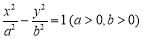 上除頂點外的任意一點,
上除頂點外的任意一點,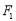 、
、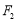 分別是雙曲線的左、右焦點,△
分別是雙曲線的左、右焦點,△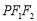 的內切圓與邊
的內切圓與邊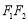 相切于點M,則
相切于點M,則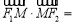 ( )
( )
(A) (B)
(B)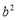 (C)
(C) (D)
(D)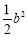
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省資陽市高三下學期4月高考模擬考試文科數學試卷(解析版) 題型:填空題
頂點在原點,對稱軸是y軸,并且經過點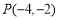 的拋物線方程是__________.
的拋物線方程是__________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三二診模擬理科數學試卷(解析版) 題型:填空題
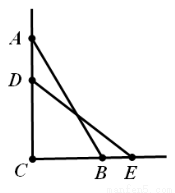
如圖,一根長為2米的木棒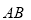 斜靠在墻壁AC上,
斜靠在墻壁AC上,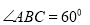 ,若
,若 滑動至
滑動至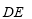 位置, 且
位置, 且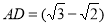 米,問木棒
米,問木棒 中點O所經過的路程為 米.
中點O所經過的路程為 米.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com