
已知 .
.
當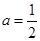 時,解不等式
時,解不等式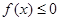 ;
;
(2)若 ,解關于
,解關于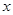 的不等式
的不等式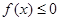 .
.
(1) ;(2)當
;(2)當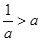 時,不等式的解集為
時,不等式的解集為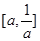 ;當
;當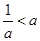 時,不等式的解集為
時,不等式的解集為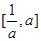 ;
;
當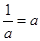 時,等式的解集為
時,等式的解集為 .
.
解析試題分析:(1)當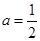 ,
,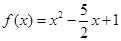 ,令
,令 ,則
,則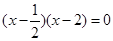 ,則由一元二次不等式與二次函數及一元二次方程三者之間的關系可知,不等式的解集為
,則由一元二次不等式與二次函數及一元二次方程三者之間的關系可知,不等式的解集為 ;(2)一元二次方程
;(2)一元二次方程 的兩根為
的兩根為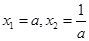 ,根據一元二次不等式與一元二次方程之間的關系可知,需對
,根據一元二次不等式與一元二次方程之間的關系可知,需對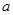 與
與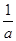 的大小關系分以下三種情況討論:當
的大小關系分以下三種情況討論:當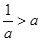 時,不等式的解集為
時,不等式的解集為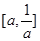 ;當
;當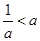 時,不等式的解集為
時,不等式的解集為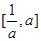 ;當
;當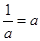 時,不等式的解集為
時,不等式的解集為 .
.
試題解析:(1)當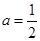 時,有不等式
時,有不等式 , 2分
, 2分
∴ ,∴不等式的解集為
,∴不等式的解集為 ; 4分
; 4分
(2)∵不等式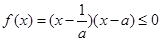 ,一元二次方程
,一元二次方程 ,兩根為
,兩根為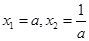 ,
,
∴當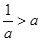 時,有
時,有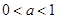 ,∴不等式的解集為
,∴不等式的解集為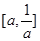 ; 7分
; 7分
當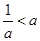 時,有
時,有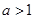 ,∴不等式的解集為
,∴不等式的解集為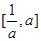 ; 10分
; 10分
當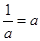 時,有
時,有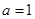 ,∴不等式的解集為
,∴不等式的解集為 . 12分
. 12分
考點:1.一元二次不等式、二次函數、一元二次方程三個二次之間的關系;2.分類討論的數學思想.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com