
【題目】已知函數(shù)![]() (
(![]() )在同一半周期內(nèi)的圖象過點
)在同一半周期內(nèi)的圖象過點![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 為函數(shù)
為函數(shù)![]() 圖象的最高點,
圖象的最高點, ![]() 為函數(shù)
為函數(shù)![]() 的圖象與
的圖象與![]() 軸的正半軸的交點,
軸的正半軸的交點, ![]() 為等腰直角三角形.
為等腰直角三角形.
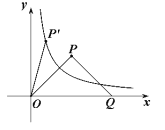
(1)求![]() 的值;
的值;
(2)將![]() 繞原點
繞原點![]() 按逆時針方向旋轉(zhuǎn)角
按逆時針方向旋轉(zhuǎn)角![]() ,得到
,得到![]() ,若點
,若點![]() 恰好落在曲線
恰好落在曲線![]() (
(![]() )上(如圖所示),試判斷點
)上(如圖所示),試判斷點![]() 是否也落在曲線
是否也落在曲線![]() (
(![]() )上,并說明理由.
)上,并說明理由.
【答案】(1)2;(2)見解析.
【解析】試題分析:(1)由已知利用周期公式可求最小正周期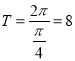 ,由題意可求Q坐標(biāo)為(4,0).P坐標(biāo)為(2,
,由題意可求Q坐標(biāo)為(4,0).P坐標(biāo)為(2, ![]() ),結(jié)合△OPQ為等腰直角三角形,即可得解
),結(jié)合△OPQ為等腰直角三角形,即可得解![]() ;
;
(2)由(Ⅰ)知, ![]() ,
, ![]() ,可求點P′,Q′的坐標(biāo),由點
,可求點P′,Q′的坐標(biāo),由點![]() 在曲線
在曲線![]() ,(x>0)上,利用倍角公式,誘導(dǎo)公式可求
,(x>0)上,利用倍角公式,誘導(dǎo)公式可求![]() ,又結(jié)合
,又結(jié)合![]() ,,可求
,,可求![]() 的值,由于
的值,由于![]() ,即可證明點Q′不落在曲線
,即可證明點Q′不落在曲線![]() (
(![]() )上.
)上.
試題解析:
(1)因為函數(shù)![]() (
(![]() )的最小正周期
)的最小正周期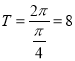 ,所以函數(shù)
,所以函數(shù)![]() 的半周期為
的半周期為![]() ,
,
所以![]() ,即有
,即有![]() 坐標(biāo)為
坐標(biāo)為![]() ,
,
又因為![]() 為函數(shù)
為函數(shù)![]() 圖象的最高點,所以點
圖象的最高點,所以點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
又因為![]() 為等腰直角三角形,所以
為等腰直角三角形,所以![]() .
.
(2)點![]() 不落在曲線
不落在曲線![]() (
(![]() )上,理由如下:
)上,理由如下:
由(1)知, ![]() ,
, ![]()
所以點![]() ,
, ![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
, ![]() .
.
因為點![]() 在曲線
在曲線![]() (
(![]() )上,所以
)上,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
又![]() .所以點
.所以點![]() 不落在曲線
不落在曲線![]() (
(![]() )上.
)上.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右頂點為
的右頂點為![]() ,上頂點為
,上頂點為![]() ,離心率
,離心率![]() ,
, ![]() 為坐標(biāo)原點,圓
為坐標(biāo)原點,圓![]() 與直線
與直線![]() 相切.
相切.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)已知四邊形![]() 內(nèi)接于橢圓
內(nèi)接于橢圓![]() .記直線
.記直線![]() 的斜率分別為
的斜率分別為![]() ,試問
,試問![]() 是否為定值?證明你的結(jié)論.
是否為定值?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著科技發(fā)展,手機成了人們?nèi)粘I钪斜夭豢缮俚耐ㄐ殴ぞ撸F(xiàn)在的中學(xué)生幾乎都擁有了屬于自己的手機了.為了調(diào)查某地區(qū)高中生一周使用手機的頻率,某機構(gòu)隨機調(diào)查了該地區(qū)100名高中生某一周使用手機的時間(單位:小時),所取樣本數(shù)據(jù)分組區(qū)間為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由此得到如圖所示的頻率分布直方圖.
,由此得到如圖所示的頻率分布直方圖.

(1)求![]() 的值并估計該地區(qū)高中生一周使用手機時間的平均值;
的值并估計該地區(qū)高中生一周使用手機時間的平均值;
(2)從使用手機時間在![]() 、
、![]() 、
、![]() 、
、![]() 的四組學(xué)生中,用分層抽樣方法抽取13人,則每層各應(yīng)抽取多少人?
的四組學(xué)生中,用分層抽樣方法抽取13人,則每層各應(yīng)抽取多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() sin 2x-cos2x-
sin 2x-cos2x-![]() ,x∈R.
,x∈R.
(1)求函數(shù)f(x)的最小值和最小正周期;
(2)設(shè)△ABC的內(nèi)角A、B、C的對邊分別為a、b、c,且c=![]() ,f(C)=0,若sin B=2sin A,求a,b的值.
,f(C)=0,若sin B=2sin A,求a,b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (m、n為常數(shù),e = 2.718 28…是自然對數(shù)的底數(shù)),曲線y = f (x)在點(1,f (1))處的切線方程是
(m、n為常數(shù),e = 2.718 28…是自然對數(shù)的底數(shù)),曲線y = f (x)在點(1,f (1))處的切線方程是![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)設(shè)![]() (其中
(其中![]() 為f (x)的導(dǎo)函數(shù)),證明:對任意x > 0,都有
為f (x)的導(dǎo)函數(shù)),證明:對任意x > 0,都有![]() .
.
(注: ![]() )
)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com