
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 上存在極大值,求
上存在極大值,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 軸是曲線
軸是曲線![]() 的一條切線,證明:當
的一條切線,證明:當![]() 時,
時,![]() .
.
 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,把滿足條件
,把滿足條件![]() 的所有數列
的所有數列![]() 構成的集合記為
構成的集合記為![]() .
.
(1)若數列![]() 通項為
通項為![]() ,求證:
,求證:![]() ;
;
(2)若數列![]() 是等差數列,且
是等差數列,且![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 的各項均為正數,且
的各項均為正數,且![]() ,數列
,數列![]() 中是否存在無窮多項依次成等差數列,若存在,給出一個數列
中是否存在無窮多項依次成等差數列,若存在,給出一個數列![]() 的通項;若不存在,說明理由.
的通項;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個圓內有6000個點,其中任三點都不共線;①能否把這個圓分成2000塊,使每塊恰含有三個點,如何分?②若每塊中三點滿足:兩兩間的距離皆為整數且不超過9,則以每塊中的三點為頂點作三角形,這些三角形中大小完全一樣的三角形至少有多少個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了豐富學生的課外文化生活,某中學積極探索開展課外文體活動的新途徑及新形式,取得了良好的效果.為了調查學生的學習積極性與參加文體活動是否有關,學校對200名學生做了問卷調查,列聯表如下:
參加文體活動 | 不參加文體活動 | 合計 | |
學習積極性高 | 80 | ||
學習積極性不高 | 60 | ||
合計 | 200 |
已知在全部200人中隨機抽取1人,抽到學習積極性不高的學生的概率為![]() .
.
(1)請將上面的列聯表補充完整;
(2)是否有99.9%的把握認為學習積極性高與參加文體活動有關?請說明你的理由;
(3)若從不參加文體活動的同學中按照分層抽樣的方法選取5人,再從所選出的5人中隨機選取2人,求至少有1人學習積極性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
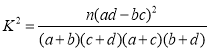 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】探月工程“嫦娥四號”探測器于2018年12月8日成功發射,實現了人類首次月球背面軟著陸.以嫦娥四號為任務圓滿成功為標志,我國探月工程四期和深空探測工程全面拉開序幕.根據部署,我國探月工程到2020年前將實現“繞、落、回”三步走目標.為了實現目標,各科研團隊進行積極的備戰工作.某科研團隊現正準備攻克甲、乙、丙三項新技術,甲、乙、丙三項新技術獨立被攻克的概率分別為![]() ,若甲、乙、丙三項新技術被攻克,分別可獲得科研經費
,若甲、乙、丙三項新技術被攻克,分別可獲得科研經費![]() 萬,
萬,![]() 萬,
萬,![]() 萬.若其中某項新技術未被攻克,則該項新技術沒有對應的科研經費.
萬.若其中某項新技術未被攻克,則該項新技術沒有對應的科研經費.
(1)求該科研團隊獲得![]() 萬科研經費的概率;
萬科研經費的概率;
(2)記該科研團隊獲得的科研經費為隨機變量![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自出生之日起,人的情緒、體力、智力等心理、生理狀況就呈周期變化,變化由線為![]() .根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
.根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
(1)請寫出小英的體力、情緒和智力節律曲線的函數;
(2)試判斷小英在2019年4月22日三種節律各處于什么階段,當日小英是否適合參加某項體育競技比賽?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種工業機器生產商,對一次性購買2臺機器的客戶,推出兩種超過質保期后兩年內的延保維修優惠方案:
方案一:交納延保金700元,在延保的兩年內可免費維修2次,超過2次每次收取維修費200元;
方案二:交納延保金1000元,在延保的兩年內可免費維修4次,超過4次每次收取維修費100元.
某工廠準備一次性購買2臺這種機器.現需決策在購買機器時應購買哪種延保方案,為此搜集并整理了50臺這種機器超過質保期后延保兩年內維修的次數,得下表:
維修次數 | 0 | 1 | 2 | 3 |
臺數 | 5 | 20 | 10 | 15 |
以這50臺機器維修次數的頻率代替1臺機器維修次數發生的概率.記X表示這2臺機器超過質保期后延保的兩年內共需維修的次數.
(1)求X的分布列;
(2)以所需延保金及維修費用的期望值為決策依據,工廠選擇哪種延保方案更合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com