Question

4．如圖，已知⊙C：x²+（y-2）²=1，點M在x軸正半軸上，過點M作⊙C的兩條切線，切點分別為A，B．
（1）若點M的坐標為（2，0），求$\overrightarrow{MA}$•$\overrightarrow{MB}$的值；
（2）若|AB|=$\frac{4\sqrt{2}}{3}$，求點M的坐標．

Answer 1

分析 （1）連結AC，BC，MC，由點C，M的坐標求得|CM|=2$\sqrt{2}$．又|CA|=1，由勾股定理求得|AM|．設∠AMC=θ，求得sin θ=$\frac{1}{2\sqrt{2}}$，利用二倍角的余弦得cos 2θ，代入數量積公式求得$\overrightarrow{MA}$•$\overrightarrow{MB}$；
（2）設點M（m，0）（m＞0），則|CM|=$\sqrt{{m}^{2}+4}$，求出|AM|．設AB與CM相交于D，則D為AB的中點，且AD⊥CM．由射影定理列式求得m，則點M的坐標可求．

解答 解：（1）連結AC，BC，MC，則AC⊥AM，BC⊥BM，△AMC≌△BMC．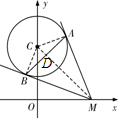
∵點C（0，2），M（2，0），∴|CM|=2$\sqrt{2}$．
又|CA|=1，∴|AM|=$\sqrt{|CM{|}^{2}-|CA{|}^{2}}$=$\sqrt{7}$．
設∠AMC=θ，則sin θ=$\frac{|CA|}{|CM|}$=$\frac{1}{2\sqrt{2}}$，cos2θ=1-2sin²θ=$\frac{3}{4}$，
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=|$\overrightarrow{MA}$||$\overrightarrow{MB}$|cos2θ=7×$\frac{3}{4}$=$\frac{21}{4}$；
（2）設點M（m，0）（m＞0），則|CM|=$\sqrt{{m}^{2}+4}$，
|AM|=$\sqrt{|CM{|}^{2}-|CA{|}^{2}}=\sqrt{{m}^{2}+3}$．
設AB與CM相交于D，則D為AB的中點，且AD⊥CM．
∴|CM|×|AD|=|CA|×|AM|，即$\sqrt{{m}^{2}+4}$×$\frac{2\sqrt{2}}{3}$=1×$\sqrt{{m}^{2}+3}$．
則8（m²+4）=9（m²+3），
∴m²=5，得m=$\sqrt{5}$，
∴點M的坐標為（$\sqrt{5}$，0）．

點評 本題考查直線與圓位置關系的應用，考查平面向量的數量積運算，考查數形結合的解題思想方法，是中檔題．