【題目】已知關于x的一元二次函數
，分別從集合P和Q中隨機取一個數a和b得到數對
。
（1）若
，
，求函數
在
內是偶函數的概率；
（2）若，，求函數有零點的概率；
（3）若
，
，求函數在區間
上是增函數的概率。
【答案】（1）
；（2）
；（3）
.
【解析】試題分析：（1）寫出所有基本事件，分析函數是偶函數所包含的基本事件即可求解；（2）寫出所有基本事件，分析函數有零點，即
包含的基本事件即可；（3）函數是增函數需要
，利用幾何概型求解即可。
試題解析：（1）由已知得， 
，所有的有序數列有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共有18對，要使
是偶函數 ,須有
滿足條件的有序數對有
，，共有3對，
．
（2）由已知得， ,所有的有序數列有，，，，，，，，，，，，，，，，，，共有18對,要使有零點 
,
滿足條件的有序數對有，，，，，共有6對,
．
（3）要使
單調遞增，
即，
可看成是平面區域
中的所有點，
而滿足條件是在平面區域
中的所有點，
．
名師指導期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】某奧運會主體育場的簡化鋼結構俯視圖如圖所示，內外兩圈的鋼骨架是離心率相同的橢圓，我們稱這兩個橢圓相似。
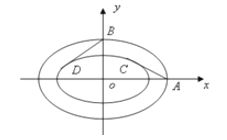
（1）已知橢圓
，寫出與橢圓
相似且焦點在
軸上、短半軸長為
的橢圓
的標準方程；若在橢圓
上存在兩點
、
關于直線
對稱，求實數
的取值范圍；
（2）從外層橢圓頂點A、B向內層橢圓引切線AC、BD，設內層橢圓方程為
+
=1 (a
b
0)，AC與BD的斜率之積為－
，求橢圓的離心率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2sin2（ 
+x）+ 
（sin2x﹣cos2x），x∈[ ， 
]．
（1）求 
的值；
（2）求f（x）的單調區間；
（3）若不等式|f（x）﹣m|＜2恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在R上的函數y=f（x）是減函數，且對任意的a∈R，都有f（﹣a）+f（a）=0，若x、y滿足不等式f（x2﹣2x）+f（2y﹣y2）≤0，則當1≤x≤4時，x﹣3y的最大值為（ ）
A.10
B.8
C.6
D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個包裝箱內有6件產品，其中4件正品，2件次品。現隨機抽出兩件產品.（要求羅列出所有的基本事件）
（1）求恰好有一件次品的概率。
（2）求都是正品的概率。
（3）求抽到次品的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱 
中，側面
和側面
都是矩形， 
是邊長為
的正三角形， 
分別為
的中點.
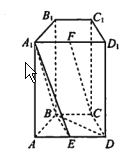
（1）求證： 
平面
；
（2）求證：平面
平面
.
（3）若
平面
，求棱
的長度.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某科研機構研發了某種高新科技產品，現已進入實驗階段.已知實驗的啟動資金為10萬元，從實驗的第一天起連續實驗，第
天的實驗需投入實驗費用為
元
，實驗30天共投入實驗費用17700元.
（1）求
的值及平均每天耗資最少時實驗的天數；
（2）現有某知名企業對該項實驗進行贊助，實驗
天共贊助
元
.為了保證產品質量，至少需進行50天實驗，若要求在平均每天實際耗資最小時結束實驗，求
的取值范圍.（實際耗資=啟動資金+試驗費用-贊助費）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
