Question

某單位投資生產A產品時，每生產1百噸需要資金2百萬元，需場地2百平方米，可獲利潤3百萬元；投資生產B產品時，每生產1百噸需要資金3百萬元，需場地1百平方米，可獲利潤2百萬元．現該單位有可使用資金14百萬元，場地9百平方米，如果利用這些資金和場地用來生產A、B兩種產品，那么分別生產A、B兩種產品各多少時，可獲得最大利潤？最大利潤是多少？

Answer 1

分析：由投資生產A產品時，每生產1百噸需要資金2百萬元，需場地2百平方米，可獲利潤3百萬元；投資生產B產品時，每生產1百米需要資金3百萬元，需場地1百平方米，可獲利潤2百萬元．現該單位有可使用資金14百萬元，場地9百平方米，我們設生產A產品x百噸，生產B產品y百米，共獲得利潤S百萬元，我們可以得到滿足條件的約束條件和目標函數，然后利用線性規劃來解答即可得到答案．

解答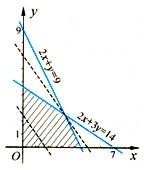：解：設生產A產品x百噸，生產B產品y百米，共獲得利潤S百萬元，（1分）
則

2x+3y≤14 2x+y≤9 x≥0 y≥0

（5分）
目標函數為S=3x+2y，
作出可行域如圖（6分）
由

2x+y=9 2x+3y=14

解得直線與2x+y=9和2x+3y=14的交點為(

13

4

，

5

2

)（7分）
平移直線y=-

3

2

x+

S

2

，當它經過直線與2x+y=9和2x+3y=14的交點(

13

4

，

5

2

)時，
直線y=-

3

2

x+

S

2

在y軸上截距

S

2

最大，S也最大． （9分）
此時，S=3×

13

4

+2×

5

2

=14.75． （10分）
因此，生產A產品3.25百噸，生產B產品2.5百米，可獲得最大利潤，最大利潤為1475萬元． （12分）

點評：本題考查的知識點是簡單線性規劃的應用，根據已知條件的限制條件，構造出約束條件和目標函數是解答此類問題的關鍵．