
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
![]() 當
當![]() 時,求函數
時,求函數![]() 的單調區間,并求出其極值;
的單調區間,并求出其極值;
![]() 若函數
若函數![]() 存在兩個零點,求k的取值范圍.
存在兩個零點,求k的取值范圍.
【答案】(1)單調增區間為(-∞,-1)和(0,+∞);單調減區間為(-1,0).極大值為![]() ;極小值為f(0)=0.(2)(-∞,0).
;極小值為f(0)=0.(2)(-∞,0).
【解析】
(1)先求導數,再求導函數零點,根據導函數符號變化規律,確定單調區間與極值,(2)先求導數,再結合導函數零點,根據k的值分五種情況分類討論,結合對應函數單調性以及極值正負確定零點個數,即得結果.
解:(1)當k=1時,![]() ,
,
∴f'(x)=(x+1)ex-(x+1)=(x+1)(ex-1),
故x∈(-∞,-1)時,f′(x)>0,f(x)為增函數;
x∈(-1,0)時,f′(x)<0,f(x)為減函數;
x∈(0,+∞)時,f'(x)>0,f(x)為增函數.
故函數f(x)的單調增區間為(-∞,-1)和(0,+∞);單調減區間為(-1,0).
所以函數的極大值為![]() ;極小值為f(0)=0.
;極小值為f(0)=0.
(2)由已知,![]() ,g(x)=kex-x,
,g(x)=kex-x,
∴![]() ,
,
∴F'(x)=kxex-x=x(kex-1).
①當k<0時,F(x)在(-∞,0)為增,在(0,+∞)為減,且注意到F(0)=-k>0,函數F(x)的圖象兩邊向下無限伸展,故此時F(x)存在兩個零點,適合題意.
②當k=0時,![]() 在(-∞,0)為增,在(0,+∞)為減,且F(0)=0,故此時F(x)只有一個零點.
在(-∞,0)為增,在(0,+∞)為減,且F(0)=0,故此時F(x)只有一個零點.
③當k=1時,![]() ,故函數(-∞,+∞)為增,易知函數F(x)只有一個零點.
,故函數(-∞,+∞)為增,易知函數F(x)只有一個零點.
④當k∈(0,1)時,![]() ,F(x)在(-∞,0)為增,
,F(x)在(-∞,0)為增,![]() 為減,
為減,![]() 為增,且F(0)=-k<0易知F(x)只有一個零點.
為增,且F(0)=-k<0易知F(x)只有一個零點.
⑤當k∈(1,+∞)時,![]() ,F(x)在
,F(x)在![]() 為增,
為增,![]() 為減,(0,+∞)為增,且
為減,(0,+∞)為增,且 ,F(0)=-k<0易知F(x)只有一個零點.
,F(0)=-k<0易知F(x)只有一個零點.
綜上,k的取值范圍是(-∞,0).


 互動英語系列答案
互動英語系列答案科目:高中數學 來源: 題型:
【題目】某學校為擔任班主任的教師辦理手機語音月卡套餐,為了解通話時長,采用隨機抽樣的方法,得到該校100位班主任每人的月平均通話時長![]() (單位:分鐘)的數據,其頻率分布直方圖如圖所示,將頻率視為概率.
(單位:分鐘)的數據,其頻率分布直方圖如圖所示,將頻率視為概率.
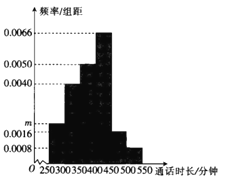
(1)求圖中![]() 的值;
的值;
(2)估計該校擔任班主任的教師月平均通話時長的中位數;
(3)在![]() ,
,![]() 這兩組中采用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求抽取的2人恰在同一組的概率.
這兩組中采用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求抽取的2人恰在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若存在實數![]() 使得
使得![]() 則稱
則稱![]() 是區間
是區間![]() 的
的![]() 一內點.
一內點.
(1)求證:![]() 的充要條件是存在
的充要條件是存在![]() 使得
使得![]() 是區間
是區間![]() 的
的![]() 一內點;
一內點;
(2)若實數![]() 滿足:
滿足:![]() 求證:存在
求證:存在![]() ,使得
,使得![]() 是區間
是區間![]() 的
的![]() 一內點;
一內點;
(3)給定實數![]() ,若對于任意區間
,若對于任意區間![]() ,
,![]() 是區間的
是區間的![]() 一內點,
一內點,![]() 是區間的
是區間的![]() 一內點,且不等式
一內點,且不等式![]() 和不等式
和不等式![]() 對于任意
對于任意![]() 都恒成立,求證:
都恒成立,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 為兩條不同的直線,
為兩條不同的直線, ![]() ,
, ![]() 為兩個不同的平面,對于下列四個命題:
為兩個不同的平面,對于下列四個命題:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正確命題的個數有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 在統計學中,回歸分析是檢驗兩個分類變量是否有關系的一種統計方法
B. 線性回歸方程對應的直線![]() 至少經過其樣本數據點中的
至少經過其樣本數據點中的![]() ,
,![]() ,
,![]()
![]() 一個點
一個點
C. 在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
D. 在回歸分析中,相關指數![]() 為
為![]() 的模型比相關指數
的模型比相關指數![]() 為
為![]() 的模型擬合的效果差
的模型擬合的效果差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】禽流感一直在威脅我們的生活,某疾病控制中心為了研究禽流感病毒繁殖個數![]() (個)隨時間
(個)隨時間![]() (天)變化的規律,收集數據如下:
(天)變化的規律,收集數據如下:
天數 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖個數 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散點圖可看出樣本點分布在一條指數型函數![]() 的周圍.
的周圍.
保留小數點后兩位數的參考數據:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 關于
關于![]() 的回歸方程(保留小數點后兩位數字);
的回歸方程(保留小數點后兩位數字);
(2)已知![]() ,估算第四天的殘差.
,估算第四天的殘差.
參考公式: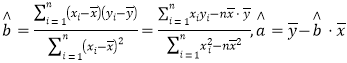
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,如果存在常數p,使得對任意正整數n,總有
,如果存在常數p,使得對任意正整數n,總有![]() 成立,那么我們稱數列
成立,那么我們稱數列![]() 為“p-擺動數列”.
為“p-擺動數列”.
(Ⅰ)設![]() ,
,![]() ,
,![]() ,判斷
,判斷![]() 、
、![]() 是否為“p-擺動數列”,并說明理由;
是否為“p-擺動數列”,并說明理由;
(Ⅱ)已知“p-擺動數列”![]() 滿足
滿足![]() ,
,![]() ,求常數p的值;
,求常數p的值;
(Ⅲ)設![]() ,且數列
,且數列![]() 的前n項和為
的前n項和為![]() ,求證:數列
,求證:數列![]() 是“p-擺動數列”,并求出常數p的取值范圍.
是“p-擺動數列”,并求出常數p的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家具公司生產甲、乙兩種書柜,制柜需先制白胚再油漆,每種柜的制造白胚工時數、油漆工時數的有關數據如下:
工藝要求 | 產品甲 | 產品乙 | 生產能力(工時/天) |
制白胚工時數 | 6 | 12 | 120 |
油漆工時數 | 8 | 4 | 64 |
單位利潤 | 20元 | 24元 |
則該公司合理安排這兩種產品的生產,每天可獲得的最大利潤為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com