

(1)在BC邊上是否存在點Q,使得PQ⊥QD?說明理由.
(2)若BC邊上有且僅有一個點Q,使PQ⊥QD,求AD與平面PDQ所成角的正弦值.
(3)在(2)的條件下,能求出平面PQD與平面PAB所成的角的大小嗎?
解:(1)假設BC邊上存在Q點,使得PQ⊥QD,則連結AQ,必有∠AQD=90°,故問題轉化為:在邊BC上是否存在點Q,使得∠AQD=90°?
由平面幾何知識,問題又可轉化為:以AD為直徑作圓,是否與BC邊有交點?
易知,當AB≤![]() AD,即a≥2時,BC邊上存在點Q,使得∠AQD=90°,從而由三垂線定理有PQ⊥QD;
AD,即a≥2時,BC邊上存在點Q,使得∠AQD=90°,從而由三垂線定理有PQ⊥QD;
當AB>![]() AD,即a<2時,不存在點Q,使得PQ⊥QD.
AD,即a<2時,不存在點Q,使得PQ⊥QD.
(2)當BC邊上有且僅有一個點Q,使得PQ⊥QD,可知BC=2,點Q為BC邊的中點.
∵DQ⊥AQ,DQ⊥PA,
∴DQ⊥平面PAQ.
∴平面PAQ⊥平面PQD.過A點作AE⊥PQ于E點,連結DE,
∴AE⊥平面PDQ.
∴∠ADE為AD與平面PDQ所成的角.
在Rt△PAQ中,PA·AQ=AE·PQ,
∴AE=![]() .
.
在Rt△AED中,sin∠ADE=![]() .
.
(3)延長DQ、AB交于F點,則二面角D—PF—A即為所求.
∵AD⊥AB,AD⊥PA,
∴AD⊥平面PAB.過A作AH⊥PF于H點,連結DH,則DH⊥PF,
∴∠DHA為二面角D—PF—A的平面角.
在Rt△PAF中,
∵AH·PF=PA·FA,
∴AH=![]() .
.
在Rt△DAH中,tan∠DHA=![]() ,
,
∴∠DHA=arctan![]() .
.
∴平面PQD與平面PAB所成角為arctan![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
A
C.2
查看答案和解析>>
科目:高中數學 來源: 題型:
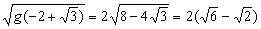
(1)若折痕所在直線的斜率為k,試寫出折痕所在直線的方程;
(2)求折痕的長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com