
【題目】某市旅游局為盡快恢復受疫情影響的旅游業,準備在本市的景區推出旅游一卡通(年卡).為了更科學的制定一卡通的有關條例,市旅游局隨機調查了2019年到本市景區旅游的1000個游客的年旅游消費支出(單位:百元),并制成如下頻率分布直方圖:
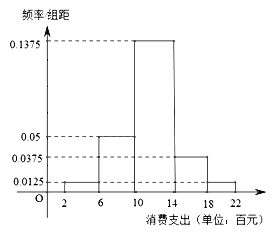
由頻率分布直方圖,可近似地認為到本市景區旅游的游客,其旅游消費支出服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() (同一組數據用該組區間的中點值作代表).
(同一組數據用該組區間的中點值作代表).
(1) 若2019年到本市景區旅游游客為500萬人,試估計2019年有多少游客在本市的年旅游消費支出不低于1820元;
(2) 現依次抽取![]() 個游客,假設每個游客的旅游消費支出相互獨立,記事件
個游客,假設每個游客的旅游消費支出相互獨立,記事件![]() 表示“連續3人的旅游消費支出超出
表示“連續3人的旅游消費支出超出![]() ”.若
”.若![]() 表示
表示![]() 的概率,
的概率,![]() 為常數),且
為常數),且![]() .
.
(ⅰ)求![]() ,
,![]() 及
及![]() ,
,![]() ;
;
(ⅱ)判斷并證明數列![]() 從第三項起的單調性,試用概率統計知識解釋其實際意義.
從第三項起的單調性,試用概率統計知識解釋其實際意義.
![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]()
【答案】(1)![]() 萬.(2)(ⅰ)
萬.(2)(ⅰ)![]() ,
,![]() ,
,![]() ,
,![]() .(ⅱ)數列
.(ⅱ)數列![]() 從第三項起單調遞減,證明見解析,用概率統計知識解釋其實際意義見解析
從第三項起單調遞減,證明見解析,用概率統計知識解釋其實際意義見解析
【解析】
(1)由直方圖求得![]() 的平均數,結合正態分布的概率計算,即可容易求得旅游費用支出不低于
的平均數,結合正態分布的概率計算,即可容易求得旅游費用支出不低于![]() 元的概率,再乘以
元的概率,再乘以![]() 即可;
即可;
(2)(ⅰ)根據題意,即可容易求得![]() ,再列出
,再列出![]() 方程,即可求得;
方程,即可求得;
(ⅱ)根據遞推公式計算![]() ,即可判斷數列的單調性;再結合實際問題,進行解釋.
,即可判斷數列的單調性;再結合實際問題,進行解釋.
(1)直方圖可得
![]()
∵![]() ,
,![]() ,
,![]()
∴旅游費用支出不低于![]() 元的概率為
元的概率為
![]() ,
,
∴![]() ,
,
估計![]() 年有
年有![]() 萬的游客在本市的年旅游費用支出不低于
萬的游客在本市的年旅游費用支出不低于![]() 元.
元.
(2)(ⅰ)![]() ,
,
![]() ,
,
所以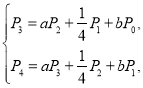
即
解得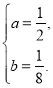
(ⅱ)數列![]() 從第三項起單調遞減
從第三項起單調遞減
![]() ,
,
故![]()
![]()
![]()
![]()
![]()
又![]() ,所以
,所以![]() ,
,
即從第三項起數列![]() 單調遞減.
單調遞減.
由此,可知隨著抽查人數![]() 的增加,事件“不連續3人的旅游費用支出超出
的增加,事件“不連續3人的旅游費用支出超出![]() ”
”
的可能性會越來越小. (即最終會出現連續3人的旅游費用支出超出![]() 這一事件)
這一事件)


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經》和《易經》里對二十四節氣的晷(guǐ)影長的記錄中,冬至和夏至的晷影長是實測得到的,其它節氣的晷影長則是按照等差數列的規律計算得出的.下表為《周髀算經》對二十四節氣晷影長的記錄,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
節氣 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 驚蟄 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (處暑) | 立夏 (立秋) | 小滿 (大暑) | 芒種 (小暑) | 夏至 |
晷影長 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易經》中記錄某年的冬至晷影長為130.0寸,夏至晷影長為14.8寸,按照上述規律那么《易經》中所記錄的春分的晷影長應為( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 與
與![]() 的交點
的交點![]() 恰好是
恰好是![]() 中點,又
中點,又![]() ,
,![]() .
.

(1)求證:![]() ;
;
(2)設![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,若直線
上,若直線![]() 平面
平面![]() ,求
,求![]() 的長;
的長;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,定義![]() 為兩點
為兩點![]() ,
,![]() 的“切比雪夫距離”,又設點
的“切比雪夫距離”,又設點![]() 及
及![]() 上任意一點
上任意一點![]() ,稱
,稱![]() 的最小值為點
的最小值為點![]() 到直線
到直線![]() 的“切比雪夫距離”,記作
的“切比雪夫距離”,記作![]() ,給出下列三個命題:
,給出下列三個命題:
①對任意三點![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
②已知點![]() 和直線
和直線![]() :
:![]() ,則
,則![]() ;
;
③到定點![]() 的距離和到
的距離和到![]() 的“切比雪夫距離”相等的點的軌跡是正方形.
的“切比雪夫距離”相等的點的軌跡是正方形.
其中正確的命題有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,
,![]() 為坐標原點.
為坐標原點.![]() 為曲線
為曲線![]() 右支上的點,點
右支上的點,點![]() 在
在![]() 外角平分線上,且
外角平分線上,且![]() .若
.若![]() 恰為頂角為
恰為頂角為![]() 的等腰三角形,則該雙曲線的離心率為( )
的等腰三角形,則該雙曲線的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】金秋九月,丹桂飄香,某高校迎來了一大批優秀的學生.新生接待其實也是和社會溝通的一個平臺.校團委、學生會從在校學生中隨機抽取了160名學生,對是否愿意投入到新生接待工作進行了問卷調查,統計數據如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根據上表說明,能否有99%把握認為愿意參加新生接待工作與性別有關;
(2)現從參與問卷調查且愿意參加新生接待工作的學生中,采用按性別分層抽樣的方法,選取10人.若從這10人中隨機選取3人到火車站迎接新生,設選取的3人中女生人數為![]() ,寫出
,寫出![]() 的分布列,并求
的分布列,并求![]() .
.
附: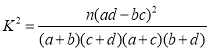 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點
的焦點![]() ,過其準線與
,過其準線與![]() 軸的交點
軸的交點![]() 作直線
作直線![]() ,
,
(1)若直線![]() 與拋物線相切于點
與拋物線相切于點![]() ,則
,則![]() =_____________.
=_____________.
(2)設![]() ,若直線
,若直線![]() 與拋物線交于點
與拋物線交于點![]() ,且
,且![]() ,則
,則![]() =_____________.
=_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查各校學生體質健康達標情況,某機構M采用分層抽樣的方法從![]() 校抽取了
校抽取了![]() 名學生進行體育測試,成績按照以下區間分為七組:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下頻率分布直方圖.根據規定,測試成績低于60分為體質不達標.已知本次測試中不達標學生共有20人.
名學生進行體育測試,成績按照以下區間分為七組:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下頻率分布直方圖.根據規定,測試成績低于60分為體質不達標.已知本次測試中不達標學生共有20人.
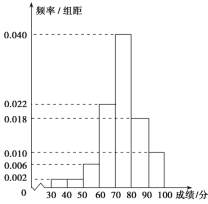
(1)求![]() 的值;
的值;
(2)現從![]() 校全體同學中隨機抽取2人,以頻率作為概率,記
校全體同學中隨機抽取2人,以頻率作為概率,記![]() 表示成績不低于90分的人數,求
表示成績不低于90分的人數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)另一機構N也對該校學生做同樣的體質達標測試,并用簡單隨機抽樣方法抽取了100名學生,經測試有20名學生成績低于60分.計算兩家機構測試成績的不達標率,你認為用哪一個值作為對該校學生體質不達標率的估計較為合理,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市教育部門為研究高中學生的身體素質與課外體育鍛煉時間的關系,對該市某校200名高中學生的課外體育鍛煉平均每天運動的時間進行調查,數據如下表:(平均每天鍛煉的時間單位:分鐘)
平均每天鍛煉的時間(分鐘) |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均課外體育運動時間在![]() 上的學生評價為“課外體育達標”.
上的學生評價為“課外體育達標”.
(1)請根據上述表格中的統計數據填寫下面![]() 列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關?
列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關?
課外體育不達標 | 課外體育達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
(2)從上述課外體育不達標的學生中,按性別用分層抽樣的方法抽取10名學生,再從這10名學生中隨機抽取3人了解他們鍛煉時間偏少的原因,記所抽取的3人中男生的人數為隨機變量為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
(3)將上述調查所得到的頻率視為概率來估計全市的情況,現在從該市所有高中學生中,抽取4名學生,求其中恰好有2名學生是課外體育達標的概率.
參考公式: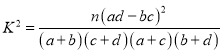 ,其中
,其中![]() .
.
參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com