
【題目】已知橢圓![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的離心率是
的離心率是![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 為橢圓長軸的左端點,
為橢圓長軸的左端點,![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點的兩點,記直線
長軸端點的兩點,記直線![]() 斜率分別為
斜率分別為![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
【答案】(1)![]() (2)過定點
(2)過定點![]()
【解析】
(1)由點M(﹣1,![]() )在橢圓C上,且橢圓C的離心率是
)在橢圓C上,且橢圓C的離心率是![]() ,列方程組求出a=2,b
,列方程組求出a=2,b![]() ,由此能求出橢圓C的標準方程.
,由此能求出橢圓C的標準方程.
(2)設點P,Q的坐標分別為(x1,y1),(x2,y2),當直線PQ的斜率存在時,設直線PQ的方程為y=kx+m,聯立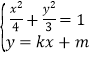 ,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判別式、韋達定理,結合已知條件得直線PQ的方程過定點(1,0);再驗證直線PQ的斜率不存在時,同樣推導出x0=1,從而直線PQ過(1,0).由此能求出直線PQ過定點(1,0).
,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判別式、韋達定理,結合已知條件得直線PQ的方程過定點(1,0);再驗證直線PQ的斜率不存在時,同樣推導出x0=1,從而直線PQ過(1,0).由此能求出直線PQ過定點(1,0).
(1)由點![]() 在橢圓
在橢圓![]() 上,且橢圓
上,且橢圓![]() 的離心率是
的離心率是![]() ,
,
可得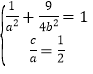 ,
,
可解得: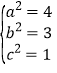
故橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)設點![]() 的坐標分別為
的坐標分別為![]() ,
,
(ⅰ)當直線![]() 斜率不存在時,由題意知,直線方程和曲線方程聯立得:
斜率不存在時,由題意知,直線方程和曲線方程聯立得:![]() ,
,![]() ,
,
(ⅱ)當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
聯立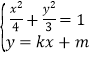 ,消去
,消去![]() 得:
得:![]() ,
,
由![]() ,有
,有![]() ,
,
由韋達定理得:![]() ,
,![]() ,
,
故![]() ,可得:
,可得:![]() ,
,
可得:![]() ,
,
整理為:![]() ,
,
故有![]() ,
,
化簡整理得:![]() ,解得:
,解得:![]() 或
或![]() ,
,
當![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() 不合題意,
不合題意,
當![]() 時直線
時直線![]() 的方程為
的方程為![]() ,即
,即![]() ,過定點
,過定點![]() ,
,
綜上,由(ⅰ)(ⅱ)知,直線![]() 過定點
過定點![]() .
.


科目:高中數學 來源: 題型:
【題目】某日A, B, C三個城市18個銷售點的小麥價格如下表:
銷售點序號 | 所屬城市 | 小麥價格(元/噸) | 銷售點序號 | 所屬城市 | 小麥價格(元/噸) |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
(Ⅰ)求B市5個銷售點小麥價格的中位數;
(Ⅱ)甲從B市的銷售點中隨機挑選一個購買1噸小麥,乙從C市的銷售點中隨機挑選一個購買1噸小麥,求甲花費的費用比乙高的概率;
(Ⅲ)如果一個城市的銷售點小麥價格方差越大,則稱其價格差異性越大.請你對A、B、C三個城市按照小麥價格差異性從大到小進行排序(只寫出結果).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣x2+ax,g(x)=ex﹣e,其中a>0.
(1)若a=1,證明:f(x)≤0;
(2)用max{m,n}表示m和n中的較大值,設函數h(x)=max{f(x),g(x)},討論函數h(x)在(0,+∞)上的零點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以坐標原點
),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,將函數
,將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖像.
的圖像.
(1)求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)在銳角![]() 中,角
中,角![]() 的對邊分別為
的對邊分別為![]() ,若
,若![]() ,
,![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過橢圓W:![]() 的左焦點
的左焦點![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點,其中
兩點,其中![]()
![]() ,另一條過
,另一條過![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點(不與
兩點(不與![]() 重合),且
重合),且![]() 點不與點
點不與點![]() 重合.過
重合.過![]() 作
作![]() 軸的垂線分別交直線
軸的垂線分別交直線![]() ,
,![]() 于
于![]() ,
,![]() .
.
(Ⅰ)求![]() 點坐標和直線
點坐標和直線![]() 的方程;
的方程;
(Ⅱ)求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com