
已知函數 (
(
 R).
R).
(1)當 時,求函數
時,求函數 的極值;
的極值;
(2)若函數 的圖象與
的圖象與 軸有且只有一個交點,求
軸有且只有一個交點,求 的取值范圍.
的取值范圍.
(1)當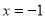 時,
時, 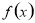 取得極大值為
取得極大值為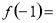
 ;
;
當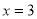 時,
時, 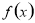 取得極小值為
取得極小值為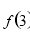
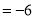 .
.
(2)a的取值范圍是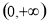 .
.
【解析】
試題分析:(1)遵循“求導數,求駐點,討論駐點兩側導數值符號,確定極值”.
(2) 根據 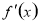 =
= 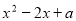 ,得到△=
,得到△= 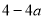 =
= 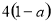 .
.
據此討論:① 若a≥1,則△≤0,
此時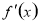 ≥0在R上恒成立,f(x)在R上單調遞增 .
≥0在R上恒成立,f(x)在R上單調遞增 .
計算f(0)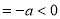 ,
,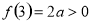 ,得到結論.
,得到結論.
② 若a<1,則△>0,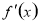 = 0有兩個不相等的實數根,不妨設為
= 0有兩個不相等的實數根,不妨設為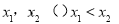 .
.
有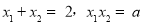 .
.
給出當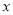 變化時,
變化時,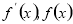 的取值情況表.
的取值情況表.
根據f(x1)·f(x2)>0, 解得a>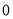 .作出結論.
.作出結論.
試題解析: (1)當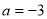 時,
時,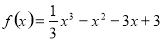 ,
,
∴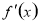
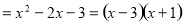 .
.
令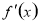 =0, 得
=0, 得 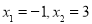 . 2分
. 2分
當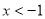 時,
時, , 則
, 則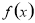 在
在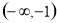 上單調遞增;
上單調遞增;
當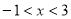 時,
時,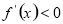 , 則
, 則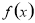 在
在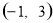 上單調遞減;
上單調遞減;
當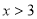 時,
時, ,
, 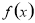 在
在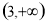 上單調遞增. 4分
上單調遞增. 4分
∴ 當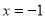 時,
時, 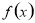 取得極大值為
取得極大值為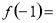
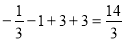 ;
;
當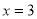 時,
時, 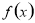 取得極小值為
取得極小值為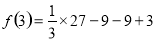
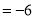 . 6分
. 6分
(2) ∵ 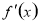 =
= 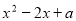 ,
,
∴△= 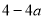 =
= 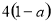 .
.
①若a≥1,則△≤0, 7分
∴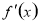 ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上單調遞增 .
∵f(0)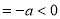 ,
,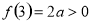 ,
,
∴當a≥1時,函數f(x)的圖象與x軸有且只有一個交點. 9分
② 若a<1,則△>0,
∴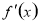 = 0有兩個不相等的實數根,不妨設為
= 0有兩個不相等的實數根,不妨設為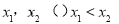 .
.
∴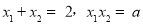 .
.
當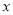 變化時,
變化時,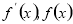 的取值情況如下表:
的取值情況如下表:
x |
| x1 | (x1,x2) | x2 |
|
| + | 0 | - | 0 | + |
f(x) | ↗ | 極大值
| ↘ | 極小值
| ↗ |
11分
∵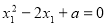 ,
,
∴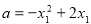 .
.
∴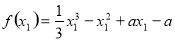
=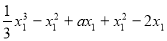
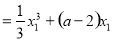
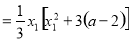 .
.
同理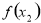
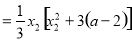 .
.
∴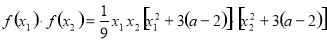
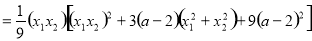
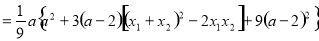
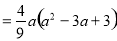 .
.
令f(x1)·f(x2)>0, 解得a>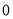 .
.
而當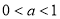 時,
時,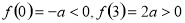 , 13分
, 13分
故當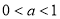 時, 函數f(x)的圖象與x軸有且只有一個交點.
時, 函數f(x)的圖象與x軸有且只有一個交點.
綜上所述,a的取值范圍是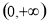 . 14分
. 14分
考點:應用導數研究函數的極值、單調性及函數的圖象,分類討論思想.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013-2014學年天津市薊縣高三第一次模擬考試理科數學試卷(解析版) 題型:選擇題
已知某程序框圖如圖所示,則該程序運行后輸出的結果為 ( )
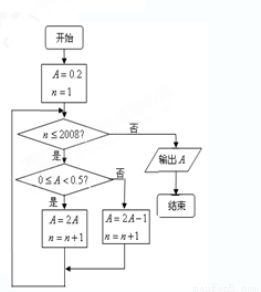
A. B.
B. C.
C.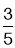 D.
D.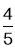
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市薊縣高三第一次模擬考試文科數學試卷(解析版) 題型:填空題
有四條線段長度分別為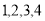 ,從這四條線段中任取三條,則所取三條線段能構成三角形的概率為 .
,從這四條線段中任取三條,則所取三條線段能構成三角形的概率為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高三5月理科數學試卷(解析版) 題型:選擇題
對任意實數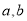 ,記
,記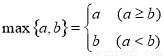 ,若
,若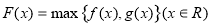 ,其中奇函數
,其中奇函數 在
在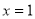 時有極小值
時有極小值 ,
, 是正比例函數,
是正比例函數,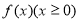 與
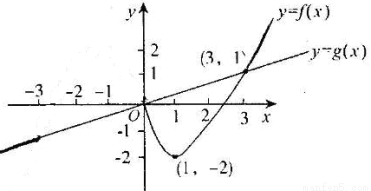
與 圖象如圖,則下列關于
圖象如圖,則下列關于 的說法中正確的是( )
的說法中正確的是( )
A.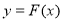 是奇函數
是奇函數
B.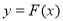 有極大值
有極大值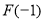 和極小值
和極小值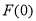
C.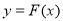 的最小值為
的最小值為 ,最大值為2
,最大值為2
D. 在
在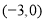 上是增函數
上是增函數
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高三5月文科數學試卷(解析版) 題型:填空題
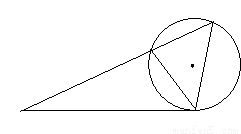
如圖,圓O是△ABC的外接圓,過點C的切線交AB的延長線于點D,CD= ,AB =3.則BD的長為 .
,AB =3.則BD的長為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高考5月模擬文科數學試卷(解析版) 題型:解答題
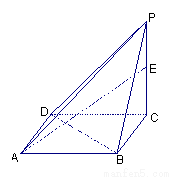
如圖,已知一四棱錐P-ABCD的底面是邊長為1的正方形,且側棱PC⊥底面ABCD,且PC=2,E是側棱PC上的動點
(1)求四棱錐P-ABCD的體積;
(2)證明:BD⊥AE。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com