
分析 (1)曲線C1的普通方程為x2+y2+2x-4=0,把x=ρcosθ,y=ρsinθ代入可得極坐標方程.曲線C2的參數(shù)方程為$\left\{\begin{array}{l}x={t^2}\\ y=t\end{array}\right.$(t為參數(shù)),消去參數(shù)t化為普通方程:x=y2,利用互化公式可得C2的極坐標方程.
(2)聯(lián)立$\left\{\begin{array}{l}{x={y}^{2}}\\{{x}^{2}+{y}^{2}+2x-4=0}\end{array}\right.$,解得交點直角坐標,再化為極坐標即可.
解答 解:(1)曲線C1的普通方程為x2+y2+2x-4=0,把x=ρcosθ,y=ρsinθ代入可得極坐標方程:ρ2+2ρcosθ-4=0.
曲線C2的參數(shù)方程為$\left\{\begin{array}{l}x={t^2}\\ y=t\end{array}\right.$(t為參數(shù)),化為普通方程:x=y2,可得C2的極坐標方程為ρcosθ=ρ2sin2θ,
即cosθ=ρsin2θ.
(2)聯(lián)立$\left\{\begin{array}{l}{x={y}^{2}}\\{{x}^{2}+{y}^{2}+2x-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
可得極坐標$(\sqrt{2},\frac{π}{4})$,$(\sqrt{2},\frac{7π}{4})$.
點評 本題考查了極坐標方程化為直角坐標方程、曲線交點、參數(shù)方程化為直角坐標,考查了推理能力與計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
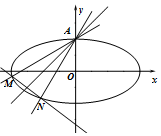 如圖,已知直線l:y=kx+1(k>0)關于直線y=x+1對稱的直線為l1,直線l,l1與橢圓E:$\frac{x^2}{4}+{y^2}$=1分別交于點A、M和A、N,記直線l1的斜率為k1.
如圖,已知直線l:y=kx+1(k>0)關于直線y=x+1對稱的直線為l1,直線l,l1與橢圓E:$\frac{x^2}{4}+{y^2}$=1分別交于點A、M和A、N,記直線l1的斜率為k1.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
| 投資股市 | 獲利40% | 不賠不賺 | 虧損20% | 購買基金 | 獲利20% | 不賠不賺 | 虧損10% |
| 概率P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ | 概率P | p | $\frac{1}{3}$ | q |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | a≥0 | B. | b≤0 | C. | c=0 | D. | a-2b+c=0 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | ∅ | B. | (-2,3) | C. | (-2,4) | D. | (-2,2) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | (0,1) | B. | $[\frac{1}{3}$,+∞) | C. | (0,$\frac{1}{3}]$ | D. | (0,$\frac{2}{3}]$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com