
【題目】記不等式組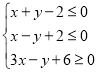 ,表示的平面區(qū)域為
,表示的平面區(qū)域為![]() .下面給出的四個命題:
.下面給出的四個命題:![]() ;
;![]() ;
;![]() ;
;![]() 其中真命題的是:
其中真命題的是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由約束條件作出可行域,利用目標函數(shù)的幾何意義求解z=x+y,z1=2x﹣y,z2![]() ,z3=x2+y2,的范圍,判斷命題的真假即可.
,z3=x2+y2,的范圍,判斷命題的真假即可.
實數(shù)x,y滿足 ,由約束條件作出可行域為D,如圖陰影部分,
,由約束條件作出可行域為D,如圖陰影部分,
A(﹣2,0),B(0,2),C(﹣1,3),z=x+y經(jīng)過可行域的點A及直線BC時分別取得最值,可得:z∈[﹣2,2],所以![]() 錯誤;
錯誤;
z1=2x﹣y經(jīng)過可行域的B、C時分別取得最值,可得:z1∈[﹣5,﹣2],所以![]() 正確;
正確;
z2![]() ,它的幾何意義是可行域內(nèi)的點與(1,﹣1)連線的斜率,
,它的幾何意義是可行域內(nèi)的點與(1,﹣1)連線的斜率,
可得:DA的斜率是最大值為:![]() ;
;
BD的斜率取得最小值為:![]() ;z2∈[
;z2∈[![]() ,
,![]() ];所以
];所以![]() 錯誤;
錯誤;
z3=x2+y2,它的幾何意義是可行域內(nèi)的點與(0,0)連線的距離的平方,
最小值為原點到直線y=x+2的距離的平方:(![]() )2
)2![]() ,最大值為OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[
,最大值為OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[![]() ,10].所以
,10].所以![]() 正確;
正確;
故選:C.



科目:高中數(shù)學(xué) 來源: 題型:
【題目】為踐行“綠水青山就是金山銀山”的發(fā)展理念,某城區(qū)對轄區(qū)內(nèi)![]() ,
,![]() ,
,![]() 三類行業(yè)共200個單位的生態(tài)環(huán)境治理成效進行了考核評估,考評分數(shù)達到80分及其以上的單位被稱為“星級”環(huán)保單位,未達到80分的單位被稱為“非星級”環(huán)保單位.現(xiàn)通過分層抽樣的方法獲得了這三類行業(yè)的20個單位,其考評分數(shù)如下:
三類行業(yè)共200個單位的生態(tài)環(huán)境治理成效進行了考核評估,考評分數(shù)達到80分及其以上的單位被稱為“星級”環(huán)保單位,未達到80分的單位被稱為“非星級”環(huán)保單位.現(xiàn)通過分層抽樣的方法獲得了這三類行業(yè)的20個單位,其考評分數(shù)如下:
![]() 類行業(yè):85,82,77,78,83,87;
類行業(yè):85,82,77,78,83,87;
![]() 類行業(yè):76,67,80,85,79,81;
類行業(yè):76,67,80,85,79,81;
![]() 類行業(yè):87,89,76,86,75,84,90,82.
類行業(yè):87,89,76,86,75,84,90,82.
(Ⅰ)計算該城區(qū)這三類行業(yè)中每類行業(yè)的單位個數(shù);
(Ⅱ)若從抽取的![]() 類行業(yè)這6個單位中,再隨機選取3個單位進行某項調(diào)查,求選出的這3個單位中既有“星級”環(huán)保單位,又有“非星級”環(huán)保單位的概率.
類行業(yè)這6個單位中,再隨機選取3個單位進行某項調(diào)查,求選出的這3個單位中既有“星級”環(huán)保單位,又有“非星級”環(huán)保單位的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x3-3x及y=f(x)上一點P(1,-2),過點P作直線l.
(1)求使直線l和y=f(x)相切且以P為切點的直線方程;
(2)求使直線l和y=f(x)相切且切點異于點P的直線方程y=g(x).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)![]() 在
在![]() 處取得極值,對
處取得極值,對![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義:若整數(shù)![]() 滿足:
滿足:![]() ,稱
,稱![]() 為離實數(shù)
為離實數(shù)![]() 最近的整數(shù),記作
最近的整數(shù),記作![]() .給出函數(shù)
.給出函數(shù)![]() 的四個命題:
的四個命題:
①函數(shù)![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ;
;
②函數(shù)![]() 是周期函數(shù),最小正周期為
是周期函數(shù),最小正周期為![]() ;
;
③函數(shù)![]() 在
在![]() 上是增函數(shù);
上是增函數(shù);
④函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱.
對稱.
其中所有的正確命題的序號為()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市春節(jié)期間7家超市的廣告費支出![]() (萬元)和銷售額
(萬元)和銷售額![]() (萬元)數(shù)據(jù)如下:
(萬元)數(shù)據(jù)如下:
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
參數(shù)數(shù)據(jù)及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,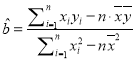 ,
,![]() ,
,![]() .
.
(1)若用線性回歸模型擬合y與x的關(guān)系,求y關(guān)于x的線性回歸方程;
(2)用對數(shù)回歸模型擬合y與x的關(guān)系,可得回歸方程:![]() ,經(jīng)計算得出線性回歸模型和對數(shù)模型的
,經(jīng)計算得出線性回歸模型和對數(shù)模型的![]() 分別約為0.75和0.97,請用
分別約為0.75和0.97,請用![]() 說明選擇哪個回歸模型更合適,并用此模型預(yù)測A超市廣告費支出為8萬元時的銷售額.
說明選擇哪個回歸模型更合適,并用此模型預(yù)測A超市廣告費支出為8萬元時的銷售額.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標系中,曲線![]() 的方程為
的方程為![]() ,以極點為原點,極軸所在直線為
,以極點為原點,極軸所在直線為![]() 軸建立直角坐標,直線
軸建立直角坐標,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),
為參數(shù)),![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設(shè)點![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比數(shù)列,求
成等比數(shù)列,求![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
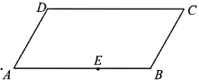
【題目】下圖是一塊平行四邊形園地![]() ,經(jīng)測量,
,經(jīng)測量,![]()
![]() .擬過線段
.擬過線段![]() 上一點
上一點![]() 設(shè)計一條直路
設(shè)計一條直路![]() (點
(點![]() 在四邊形
在四邊形![]() 的邊上,不計直路的寬度),將該園地分為面積之比為
的邊上,不計直路的寬度),將該園地分為面積之比為![]() 的左,右兩部分分別種植不同花卉.設(shè)
的左,右兩部分分別種植不同花卉.設(shè)![]() (單位:m).
(單位:m).
(1)當點![]() 與點
與點![]() 重合時,試確定點
重合時,試確定點![]() 的位置;
的位置;
(2)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)試確定點![]() 的位置,使直路
的位置,使直路![]() 的長度最短.
的長度最短.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com