
【題目】已知函數![]() (
(![]() 為自然對數的底數,
為自然對數的底數,![]() ).
).
(1)求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若對于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)對函數![]() 求導,求得
求導,求得![]() ,
,![]() ,由直線的點斜式方程可求得切線;
,由直線的點斜式方程可求得切線;
(2)對函數![]() 求導,得出函數
求導,得出函數![]() 在
在![]() 上單調性,可求得函數
上單調性,可求得函數![]() 在
在![]() 上的最值,再根據對于任意
上的最值,再根據對于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,則需
,則需![]() ,
,
討論a可求得a的范圍;
(3) )因為![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,則
,則![]() ,分析導函數的正負,得出原函數的單調性,從而得出最值,根據不等式恒成立的思想得出求得a的范圍.
,分析導函數的正負,得出原函數的單調性,從而得出最值,根據不等式恒成立的思想得出求得a的范圍.
(1)![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
所以切線方程為:![]() ,即
,即![]() ;
;
(2)![]() ,
,![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,
,
由于對于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,則需
,則需![]() ,
,
![]()
當![]() 時,
時,![]() ,不滿足
,不滿足![]() ,故
,故![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,所以
,所以![]()
![]() ,解得
,解得![]() ;
;
當![]() 時,
時,![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() 在
在![]() 上沒有最大值,所以
上沒有最大值,所以![]() 不滿足,
不滿足,
綜上可得,![]() ;
;
(3)因為![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,則
,則![]() ,
,
令![]() 則
則![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,所以存在唯一的零點
,所以存在唯一的零點![]() ,使得
,使得![]() ,
,
即有![]() 也即有
也即有![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上遞減,所以
上遞減,所以![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() 的取值范圍是
的取值范圍是![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】據統計,某5家鮮花店今年4月的銷售額和利潤額資料如下表:
鮮花店名稱 | A | B | C | D | E |
銷售額x(千元) | 3 | 5 | 6 | 7 | 9 |
利潤額y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法計算利潤額y關于銷售額x的回歸直線方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鮮花店的銷售額為8千元時,利用(1)的結論估計這家鮮花店的利潤額是多少.
參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計值公式分別為
中斜率和截距的最小二乘法估計值公式分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]()
(1)當![]() 時,討論
時,討論![]() 的單調性
的單調性
(2)當![]() 時,是否存在整數
時,是否存在整數![]() 使得關于
使得關于![]() 的不等式
的不等式![]() 在區間
在區間![]() 內有解?若存在,求出整數
內有解?若存在,求出整數![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電子芯片是“中國智造”的靈魂,是所有整機設備的“心臟”.某國產電子芯片公司,通過大數據分析,得到如下規律:生產一種高端芯片x(![]() )萬片,其總成本為
)萬片,其總成本為![]() ,其中固定成本為800萬元,并且每生產1萬片的生產成本為200萬元(總成本=固定成本+生產成本),銷售收入
,其中固定成本為800萬元,并且每生產1萬片的生產成本為200萬元(總成本=固定成本+生產成本),銷售收入![]() (單位:萬元)滿足
(單位:萬元)滿足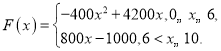 假定生產的芯片都能賣掉.
假定生產的芯片都能賣掉.
(1)將利潤![]() (單位:萬元)表示為產量x(單位:萬片)的函數;
(單位:萬元)表示為產量x(單位:萬片)的函數;
(2)當產量x(單位:萬片)為何值時,公司所獲利潤最大?最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
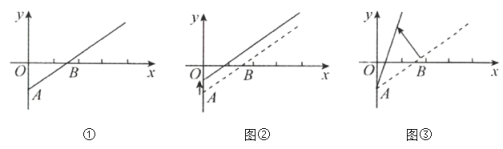
【題目】如圖①是反映某條公交線路收支差額(即營運所得票價收入與付出成本的差)![]() 與乘客量
與乘客量![]() 之間關系的圖像.由于目前該條公交線路虧損,公司有關人員提出了兩種調整的建議,如圖②③所示:
之間關系的圖像.由于目前該條公交線路虧損,公司有關人員提出了兩種調整的建議,如圖②③所示:
給出下列說法:(1)圖②的建議:提高成本,并提高票價;(2)圖②的建議:降低成本,并保持票價不變;(3)圖③的建議:提高票價,并保持成本不變;(4)圖③的建議:提高票價,并降低成本.其中所有說法正確的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一汽車廠生產![]() ,
,![]() ,
,![]() 三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有
三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有![]() 類轎車10輛.
類轎車10輛.
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分層抽樣的方法在![]() 類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
(3)用隨機抽樣的方法從![]() 類舒適型轎車中抽取8輛,經檢測它們的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把這8輛轎車的得分看作一個總體,從中任取一個得分數
類舒適型轎車中抽取8輛,經檢測它們的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把這8輛轎車的得分看作一個總體,從中任取一個得分數![]() ,記這8輛轎車的得分的平均數為
,記這8輛轎車的得分的平均數為![]() ,定義事件
,定義事件![]() ,且函數
,且函數![]() 沒有零點
沒有零點![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f1(x),y=f2(x),定義函數f(x)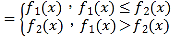 .
.
(1)設函數f1(x)=x+3,f2(x)=x2﹣x,求函數y=f(x)的解析式;
(2)在(1)的條件下,g(x)=mx+2(m∈R),函數h(x)=f(x)﹣g(x)有三個不同的零點,求實數m的取值范圍;
(3)設函數f1(x)=x2﹣2,f2(x)=|x﹣a|,函數F(x)=f1(x)+f2(x),求函數F(x)的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com