
【題目】已知點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,依據圖像可知,線段
的圖像上任意不同的兩點,依據圖像可知,線段![]() 總是位于
總是位于![]() 兩點之間函數圖像的上方,因此有結論
兩點之間函數圖像的上方,因此有結論![]() 成立,運用類比的思想方法可知,若點
成立,運用類比的思想方法可知,若點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,則類似地有_________成立.
的圖像上任意不同的兩點,則類似地有_________成立.
 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】大豆是我國主要的農作物之一,因此,大豆在農業發展中占有重要的地位,隨著農業技術的不斷發展,為了使大豆得到更好的種植,就要進行超級種培育研究.某種植基地培育的“超級豆”種子進行種植測試:選擇一塊營養均衡的可種植![]() 株的實驗田地,每株放入三粒“超級豆”種子,且至少要有一粒種子發芽這株豆苗就能有效成活,每株豆成活苗可以收成大豆
株的實驗田地,每株放入三粒“超級豆”種子,且至少要有一粒種子發芽這株豆苗就能有效成活,每株豆成活苗可以收成大豆![]() .已知每粒豆苗種子成活的概率為
.已知每粒豆苗種子成活的概率為![]() (假設種子之間及外部條件一致,發芽相互沒有影響).
(假設種子之間及外部條件一致,發芽相互沒有影響).
(Ⅰ)求恰好有3株成活的概率;
(Ⅱ)記成活的豆苗株數為![]() ,收成為
,收成為![]() ,求隨機變量
,求隨機變量![]() 分布列及
分布列及![]() 數學期望
數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC![]() 中,側面
中,側面![]() 是矩形,∠BAC=90°,
是矩形,∠BAC=90°,![]() ⊥BC,
⊥BC,![]() =AC=2AB=4,且
=AC=2AB=4,且![]() ⊥
⊥![]() .
.

(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)設D是![]() 的中點,判斷并證明在線段
的中點,判斷并證明在線段![]() 上是否存在點E,使得DE∥平面
上是否存在點E,使得DE∥平面![]() .若存在,求二面角E
.若存在,求二面角E![]() B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 具有性質:若
具有性質:若![]() 、
、![]() 是雙曲線左、右頂點,
是雙曲線左、右頂點,![]() 為雙曲線上一點,且
為雙曲線上一點,且![]() 在第一象限.記直線
在第一象限.記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,那么
,那么![]() 與
與![]() 之積是與點
之積是與點![]() 位置無關的定值.
位置無關的定值.
(1)試對橢圓![]() ,類比寫出類似的性質(不改變原有命題的字母次序),并加以證明.
,類比寫出類似的性質(不改變原有命題的字母次序),并加以證明.
(2)若橢圓![]() 的左焦點
的左焦點![]() ,右準線為
,右準線為![]() ,在(1)的條件下,當
,在(1)的條件下,當![]() 取得最小值時,求
取得最小值時,求![]() 的垂心
的垂心![]() 到
到![]() 軸的距離.
軸的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
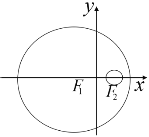
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 世紀
世紀![]() 年代,里克特(C.F.Richter)制定了一種表明地震能量大小的尺度,就是使用測震儀衡量地震能量的等級,地震能量越大,測震儀記錄的地震曲線的振幅就越大.這就是我們常說的里氏震級
年代,里克特(C.F.Richter)制定了一種表明地震能量大小的尺度,就是使用測震儀衡量地震能量的等級,地震能量越大,測震儀記錄的地震曲線的振幅就越大.這就是我們常說的里氏震級![]() ,其計算公式為:
,其計算公式為:![]() ,其中,
,其中,![]() 是被測地震的最大振幅,
是被測地震的最大振幅,![]() 是“標準地震”的振幅(使用標準地震振幅是為了修正測震儀距實際震中的距離造成的偏差).(以下數據供參考:
是“標準地震”的振幅(使用標準地震振幅是為了修正測震儀距實際震中的距離造成的偏差).(以下數據供參考:![]() ,
,![]() ,
,![]() )
)
(1)根據中國地震臺網測定,![]() 年
年![]() 月
月![]() 日
日![]() 時
時![]() 分,新疆巴音郭楞蒙古自治州若羌縣發生地震,一個距離震中
分,新疆巴音郭楞蒙古自治州若羌縣發生地震,一個距離震中![]() 千米的測震儀記錄的地震最大振幅是
千米的測震儀記錄的地震最大振幅是![]() ,此時標準地震的振幅是
,此時標準地震的振幅是![]() ,計算這次地震的震級(精確到
,計算這次地震的震級(精確到![]() );
);
(2)![]() 年
年![]() 月
月![]() 日
日![]() 時
時![]() 分
分![]() 秒在我國四川省汶川地區發生特大地震,根據中華人民共和國地震局的數據,此次地震的里氏震級達
秒在我國四川省汶川地區發生特大地震,根據中華人民共和國地震局的數據,此次地震的里氏震級達![]() ,地震烈度達到
,地震烈度達到![]() 度.此次地震的地震波已確認共環繞了地球
度.此次地震的地震波已確認共環繞了地球![]() 圈.地震波及大半個中國及亞洲多個國家和地區,北至遼寧,東至上海,南至香港、澳門、泰國、越南,西至巴基斯坦均有震感.請計算汶川地震的最大振幅是
圈.地震波及大半個中國及亞洲多個國家和地區,北至遼寧,東至上海,南至香港、澳門、泰國、越南,西至巴基斯坦均有震感.請計算汶川地震的最大振幅是![]() 級地震的最大振幅的多少倍?
級地震的最大振幅的多少倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,且橢圓的短軸長為2.
,且橢圓的短軸長為2.
(1)球橢圓的標準方程;
(2)已知直線![]() 過右焦點
過右焦點![]() ,且它們的斜率乘積為
,且它們的斜率乘積為![]() ,設
,設![]() 分別與橢圓交于點
分別與橢圓交于點![]() 和
和![]() .
.
①求![]() 的值;
的值;
②設![]() 的中點
的中點![]() ,
,![]() 的中點為,求
的中點為,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】20名高二學生某次數學考試成績(單位:分)的頻率分布直方圖如圖:
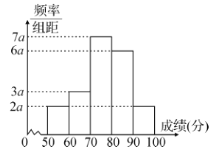
(1)求頻率分布直方圖中![]() 的值;
的值;
(2)分別求出成績落在![]() 與
與![]() 中的學生人數;
中的學生人數;
(3)從成績在![]() 的學生中任選2人,求此2人的成績都在
的學生中任選2人,求此2人的成績都在![]() 中的概率.
中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com