
【題目】今年3月10日湖北武漢某方艙醫院“關門大吉”,某省馳援湖北“抗疫”的9名身高各不相同的醫護人員站成一排合影留念,慶祝圓滿完成“抗疫”任務,若恰好從中間往兩邊看都依次變低,則身高排第4的醫護人員和最高的醫護人員相鄰的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
將身高從低到高的9個人依次編號為1,2,3,4,5,6,7,8,9,則9號定在正中間,兩邊是四個元素的定序排列,6號與9號分左右兩邊相鄰,與6在同一邊的另外3個元素(從1,2,3,4,5種任選3個)定序排列,另一邊的四個元素定序排列, 最后根據古典概型的概率公式可得答案.
身高最高
將身高從低到高的9個人依次編號為1,2,3,4,5,6,7,8,9,
則9號必須排在正中間,從其余8個人中任選4人排在9號的左邊,剩下的4個人排在9號的右邊,有![]() 種,
種,
當排名第四的6號排在最高的9號的左邊時,從1,2,3,4,5中任選3個排在6號的左邊,其余四個排在9號的右邊,有![]() 種,同理當當排名第四的6號排在最高的9號的右邊時,也有10種,
種,同理當當排名第四的6號排在最高的9號的右邊時,也有10種,
所以身高排名第四的6號與最高的9號相鄰的排法有10+10=20種,
所以身高排第4的醫護人員和最高的醫護人員相鄰的概率為![]() .
.
故選:A.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,對
,對![]() ∈[0, π],都有
∈[0, π],都有![]() ,滿足f(x2)=0的實數x有且只有3個,給出下述四個結論:①滿足題目條件的實數x0有且只有1個;②滿足題目條件的實數x1有且只有1個;③f(x)在
,滿足f(x2)=0的實數x有且只有3個,給出下述四個結論:①滿足題目條件的實數x0有且只有1個;②滿足題目條件的實數x1有且只有1個;③f(x)在![]() 上單調遞增;④
上單調遞增;④![]() 的取值范圍是
的取值范圍是![]() ;其中所有正確結論的編號是( )
;其中所有正確結論的編號是( )
A.①③B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了嚴格監控某種零件的一條生產線的生產過程,某企業每天從該生產線上隨機抽取10000個零件,并測量其內徑(單位:![]() ).根據長期生產經驗,認為這條生產線正常狀態下生產的零件的內徑
).根據長期生產經驗,認為這條生產線正常狀態下生產的零件的內徑![]() 服從正態分布
服從正態分布![]() .如果加工的零件內徑小于
.如果加工的零件內徑小于![]() 或大于
或大于![]() 均為不合格品,其余為合格品.
均為不合格品,其余為合格品.
(1)假設生產狀態正常,請估計一天內抽取的10000個零件中不合格品的個數約為多少;
(2)若生產的某件產品為合格品則該件產品盈利;若生產的某件產品為不合格品則該件產品虧損.已知每件產品的利潤![]() (單位:元)與零件的內徑
(單位:元)與零件的內徑![]() 有如下關系:
有如下關系: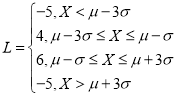 .求該企業一天從生產線上隨機抽取10000個零件的平均利潤.
.求該企業一天從生產線上隨機抽取10000個零件的平均利潤.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,有
,有![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐P ABC中,PA⊥平面ABC,![]() Q是BC邊上的一個動點,且直線PQ與面ABC所成角的最大值為
Q是BC邊上的一個動點,且直線PQ與面ABC所成角的最大值為![]() 則該三棱錐外接球的表面積為( )
則該三棱錐外接球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,E、F、G分別為AA1、BC、C1D1的中點,現有下面三個結論:①△EFG為正三角形;②異面直線A1G與C1F所成角為60°;③AC∥平面EFG.其中所有正確結論的編號是( )
A.①B.②③C.①②D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解該校學生“停課不停學”的網絡學習效率,隨機抽查了高一年級100位學生的某次數學成績,得到如圖所示的頻率分布直方圖:
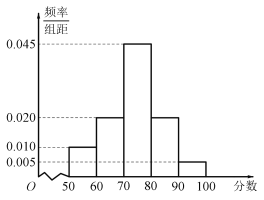
(1)估計這100位學生的數學成績的平均值![]() .(同一組中的數據用該組區間的中點值代表);
.(同一組中的數據用該組區間的中點值代表);
(2)根據整個年級的數學成績,可以認為學生的數學成績![]() 近似地服從正態分布
近似地服從正態分布![]() 經計算,(1)問中樣本標準差
經計算,(1)問中樣本標準差![]() 的近似值為10.用樣本平均數
的近似值為10.用樣本平均數![]() 作為
作為![]() 的近似值,用樣本標準差
的近似值,用樣本標準差![]() 作為
作為![]() 的估計值,現任抽取一位學生,求他的數學成績恰在64分到94分之間的概率.
的估計值,現任抽取一位學生,求他的數學成績恰在64分到94分之間的概率.
參考數據:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]()
(3)該年級1班的數學老師為了能每天督促學生的網絡學習,提高學生每天的作業質量及學習數學的積極性,特意在微信上設計了一個每日作業小程序,每當學生提交的作業獲得優秀時,就有機會參與一次小程序中“玩游戲,得獎勵積分”的活動,開學后可根據獲得積分的多少領取老師相應的小獎品.小程序頁面上有一列方格,共15格,剛開始有只小兔子在第1格,每點一下游戲的開始按鈕,小兔子就沿著方格跳一下,每次跳1格或跳2格,概率均為![]() ,依次點擊游戲的開始按鈕,直到小兔子跳到第14格(獎勵0分)或第15格(獎勵5分)時,游戲結束,每天的積分自動累加,設小兔子跳到第
,依次點擊游戲的開始按鈕,直到小兔子跳到第14格(獎勵0分)或第15格(獎勵5分)時,游戲結束,每天的積分自動累加,設小兔子跳到第![]() 格的概率為
格的概率為![]() ,試證明
,試證明![]() 是等比數列,并求
是等比數列,并求![]() 的值.(獲勝的概率)
的值.(獲勝的概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D與AD1交于點E,AA1=AD=2AB=4.
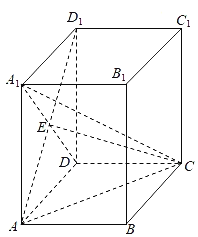
(1)證明:AE⊥平面ECD.
(2)求點C1到平面AEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,已知四邊形AA1C1C為矩形,AA1=6,AB=AC=4,∠BAC=∠BAA1=60°,∠A1AC的角平分線AD交CC1于D.
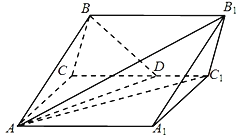
(1)求證:平面BAD⊥平面AA1C1C;
(2)求二面角A﹣B1C1﹣A1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全球抗擊新冠肺炎疫情期間,我國醫療物資生產企業加班加點生產口罩、防護服、消毒水等防疫物品,保障抗疫一線醫療物資供應,在國際社會上贏得一片贊譽.我國某口罩生產企業在加大生產的同時,狠抓質量管理,不定時抽查口罩質量,該企業質檢人員從所生產的口罩中隨機抽取了100個,將其質量指標值分成以下六組:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下頻率分布直方圖.
,得到如下頻率分布直方圖.
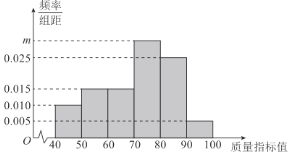
(1)求出直方圖中![]() 的值;
的值;
(2)利用樣本估計總體的思想,估計該企業所生產的口罩的質量指標值的平均數和中位數(同一組中的數據用該組區間中點值作代表,中位數精確到0.01);
(3)現規定:質量指標值小于70的口罩為二等品,質量指標值不小于70的口罩為一等品.利用分層抽樣的方法從該企業所抽取的100個口罩中抽出5個口罩,并從中再隨機抽取2個作進一步的質量分析,試求這2個口罩中恰好有1個口罩為一等品的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com