
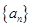 ,
,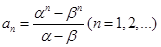 ,其中
,其中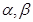 是方程
是方程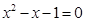 的兩個根.
的兩個根.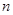 ,都有
,都有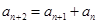 ;
;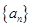 中的項都是正整數(shù),試證明:任意相鄰兩項的最大公約數(shù)均為1;
中的項都是正整數(shù),試證明:任意相鄰兩項的最大公約數(shù)均為1;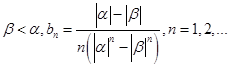 ,證明:
,證明: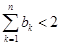 。
。 優(yōu)生樂園系列答案
優(yōu)生樂園系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
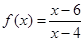
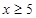 時
時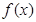 的取值范圍;
的取值范圍;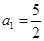 且
且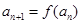 對任意
對任意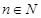 成立;
成立;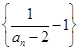 是等比數(shù)列;
是等比數(shù)列;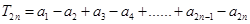 ,求證
,求證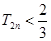 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 滿足:
滿足: ,其中
,其中 為數(shù)列
為數(shù)列 的前
的前 項和.
項和. 的通項公式;
的通項公式; ,數(shù)列
,數(shù)列 的前
的前 項和為
項和為 ,求證
,求證
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
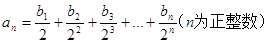 ,求數(shù)列{bn}的前n項和Sn.
,求數(shù)列{bn}的前n項和Sn.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 n∈N*, Sn,Sn+1,Sn+2不構(gòu)成等比數(shù)列.
n∈N*, Sn,Sn+1,Sn+2不構(gòu)成等比數(shù)列.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 的相鄰兩項
的相鄰兩項 是關(guān)于
是關(guān)于 的方程
的方程 的兩根,且
的兩根,且
 是等比數(shù)列;
是等比數(shù)列; 的前
的前 項和
項和 ;
; 對任意的
對任意的 都成立,求
都成立,求 的取值范圍。
的取值范圍。查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com