
 )6+x-2x2;
)6+x-2x2; )-|x|.
)-|x|. )u.則函數為單調遞減的指數函數,u為二次函數,則求出u的最大值得到y的最小即可求出值域,定義域為R,u的對稱軸求出,在對稱軸左邊函數增函數,右邊為減函數,在根據復合函數求出y的單調區間即可;
)u.則函數為單調遞減的指數函數,u為二次函數,則求出u的最大值得到y的最小即可求出值域,定義域為R,u的對稱軸求出,在對稱軸左邊函數增函數,右邊為減函數,在根據復合函數求出y的單調區間即可; )u.
)u. )2+
)2+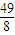 ,
, )
)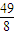 }.
}. ,
, ,+∞)上u=6+x-2x2是減函數,
,+∞)上u=6+x-2x2是減函數, ]上是增函數,又函數y=(
]上是增函數,又函數y=( )u是減函數,
)u是減函數, )6+x-2x2在[
)6+x-2x2在[ ,+∞)上是增函數,
,+∞)上是增函數, ]上是減函數.
]上是減函數. )-|x|=(
)-|x|=( )|x|≥(
)|x|≥( )=1.
)=1. )-|x|的值域為{y|y≥1}.
)-|x|的值域為{y|y≥1}. )-|x|是偶函數,
)-|x|是偶函數, )-|x|=
)-|x|=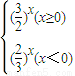 所以函數y=(
所以函數y=( )-|x|在(-∞,0]上是減函數,在[0,+∞)上是增函數.
)-|x|在(-∞,0]上是減函數,在[0,+∞)上是增函數.

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com