
(1)設x≥1,y≥1,證明x+y+ ≤
≤ +
+ +xy;
+xy;
(2)1<a≤b≤c,證明logab+logbc+logca≤logba+logcb+logac.
(1)見解析(2)見解析
【解析】(1)由于x≥1,y≥1,
要證x+y+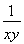 ≤
≤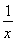 +
+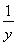 +xy,
+xy,
只需證xy(x+y)+1≤y+x+(xy)2.
因為[y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1).
由條件x≥1,y≥1,得(xy-1)(x-1)(y-1)≥0,
從而所要證明的不等式成立.
(2)設logab=x,logbc=y,由對數的換底公式得logca=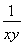 ,logba=
,logba=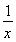 ,logcb=
,logcb= ,logac=xy.
,logac=xy.
于是,所要證明的不等式即為x+y+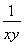 ≤
≤ +
+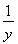 +xy.
+xy.
其中x=logab≥1,y=logbc≥1.
故由(1)可知所要證明的不等式成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2014年高考數學文復習二輪作業手冊新課標·通用版限時集14講練習卷(解析版) 題型:選擇題
已知雙曲線 =1(a>0,b>0)的一個焦點到漸近線的距離是焦距的
=1(a>0,b>0)的一個焦點到漸近線的距離是焦距的 ,則雙曲線的離心率是( )
,則雙曲線的離心率是( )
A.2 B.4 C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文復習二輪作業手冊新課標·通用版限時集11講練習卷(解析版) 題型:選擇題
某四棱錐的底面為正方形,其三視圖如圖所示,則該四棱錐的體積等于( )

A.1 B.2 C.3 D.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文復習二輪作業手冊新課標·通用版限時集10講練習卷(解析版) 題型:選擇題
若數列{cn}的通項cn=(2n-1)· ,則數列{cn}的前n項和Rn=( )
,則數列{cn}的前n項和Rn=( )
A.1- B.1-
B.1- C.1+
C.1+ D.1+
D.1+
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文二輪專題復習與測試選修4-5不等式選講練習卷(解析版) 題型:解答題
已知a,b為正實數.
(1)求證: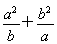 ≥a+b;
≥a+b;
(2)利用(1)的結論求函數y=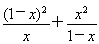 (0<x<1)的最小值.?
(0<x<1)的最小值.?
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文二輪專題復習與測試選修4-5不等式選講 練習卷(解析版) 題型:填空題
已知a,b,c∈R,a+2b+3c=6,則a2+4b2+9c2的最小值為________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文二輪專題復習與測試選修4-5不等式選講 練習卷(解析版) 題型:選擇題
“a<4”是“對任意的實數x,|2x-1|+|2x+3|≥a成立”的( )
A.充分必要條件 B.充分不必要條件
C.必要不充分條件 D.既非充分也非必要條件
查看答案和解析>>
科目:高中數學 來源:2014年高考數學文二輪專題復習與測試選修4-1幾何證明選講練習卷(解析版) 題型:解答題
如圖,AB為⊙O的直徑,直線CD與⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,連接AE,BE.證明:

(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(六)第二章第三節練習卷(解析版) 題型:填空題
已知y=f(x)+x2是奇函數,且f(1)=1,若g(x)=f(x)+2,則g(-1)= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com